Four Ideas To Deepen Student Math Discussions
This article and the free download at its conclusion are adapted from Intentional Talk: How to Structure and Lead Productive Mathematical Discussions (Stenhouse, 2014). Used with permission.

Leading mathematical discussions can be both invigorating and challenging. It’s easy to start a discussion by asking children to share their thinking. And nothing beats those moments when children proudly share something they figured out.
But then what? Math discussions aren’t just about show-and-tell: stand up, sit down, clap, clap, clap. Knowing what to do with students’ ideas and teaching children how to meaningfully participate in discussions can be a lot more daunting.
We often worry during a discussion that students might get lost trying to keep up with what everyone is saying or that they may simply tune out when a lot of ideas are shared. And no teacher likes that uncomfortable feeling of putting a child on the spot.
Yet when teachers plan for and steer productive discussions, children realize it’s worth listening to one another and that it’s okay to be pressed to say more.
Our four principles for good math discussions

Our work with classroom discussions is guided by four principles:
1. Discussions should achieve a mathematical goal, and different types of goals require planning and leading discussions differently.
2. Students need to know what and how to share so their ideas are heard and are useful to others.
3. Teachers need to orient students to one another and the mathematical ideas so that every member of the class is involved in achieving the mathematical goal.
4. Teachers must communicate that all children are sense makers and that their ideas are valued.
The classroom vignettes in our book reflect insights we have gained into leading mathematical discussions while working closely with teachers who are committed to equity in students’ achievements and learning opportunities.
These vignettes do not take place in gifted classrooms or in schools in the most affluent neighborhoods. We hope the everyday brilliance of the teachers and children shared in our book will help us all strive toward creating classrooms that disrupt longstanding assumptions about who can and cannot excel in mathematics (Delpit 2012).
Here’s a bit more about what we mean by each of the four principles. This will give you a glimpse into the ways particular mathematical goals can help you run a discussion.
Principle 1: Discussions Should Achieve a Mathematical Goal
The mathematical goal acts as your compass as you navigate classroom talk. The goal helps you decide what to listen for, which ideas to pursue, and which to highlight. In Orchestrating Productive Mathematics Discussions (2011), Margaret Smith and Mary Kay Stein describe the importance of teachers clearly specifying the mathematical goal before planning out a discussion. The mathematical ideas at the heart of a lesson will help you distinguish between different types of classroom discussions you can have with your students.
Sometimes your aim is to have students share as many different ideas as possible in the discussion so they see a range of possibilities. We call this “open strategy sharing,” because we’re working on building students’ repertoire of strategies. The class generates lots of ideas, and the discussion likely moves across a broad terrain that includes mathematical concepts, procedures, representations, and explanations. Students listen for and contribute different ways to solve the same problem.
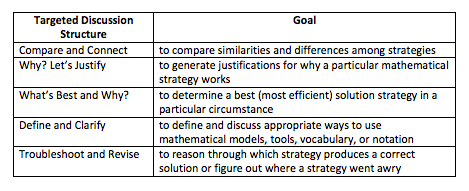
At other times you might want to focus the discussion on a particular idea. We call this “targeted discussion.” Through targeted sharing the discussion zooms in on a particular idea. This more focused sharing involves specific goals, like defining and using key terms or concepts correctly, revising an incorrect strategy, or making sense of a particular representation. The students listen to and contribute ideas in order to move toward consensus. In the table above are the targeted discussion structures that we focus on in chapters of Intentional Talk.
Principle 2: Students Need to Know What and How to Share
To make classroom discussions come alive, students need help knowing how to participate. When students have the chance to express their ideas, teachers have more information about what students do understand, what they are grappling with, and where they might be stumbling or confused.
Students learn through classroom discussions what to share. In our book, we provide guidance for how to structure each type of discussion. We also pay attention to how students learn to contribute meaningfully in different types of discussions.

We can use and offer sentence starters that cue students to know what to say: “Explain to me what you meant by ____,” “What would you do if the number was ____?” and “How is your way different from ____?”
We also help students learn what to listen for so they can contribute to the conversation: “Listen for how she broke apart the numbers,” “Think about whether you are understanding how she used the number line to show her thinking.”
Similarly, students learn how to share through our explicit support. Reinforcing norms supports students in knowing how to share. For example, you might need to reinforce where to place oneself (“Stand here so we can see your work”); how loudly to speak (“Speak loudly so everyone can hear your idea”); and what tools to use (“Use the drawing in your journal to help”).
We want to help children crack the code of being successful in meaningful mathematical learning at the same time as we tap into and draw on the resources they bring to the classroom (Aguirre, Mayfield-Ingram, and Martin 2013).
Principle 3: Teachers Need to Orient Students to One Another and the Mathematical Ideas
One of the challenges of leading discussions is bringing the whole class into the discussion. Most classrooms have several students who are eager to share and will always raise their hands and volunteer their thoughts. If we always call on these students, it’s easy for others to remain passive or become anxious about how to enter the discussion.
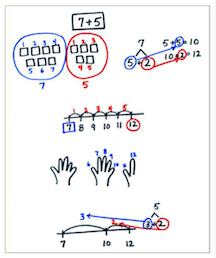
Charting students’ strategies.
But that’s not the only problem; if students have their hands raised just to get in their two cents, you’ll end up with a bunch of ideas that don’t build on each other or go anywhere. Teachers have to use strategies that help students learn how to attend to each other’s ideas and the mathematics. We call this orienting students to one another and the mathematics.
Teachers can draw attention to the meaningful contributions that all students make and can encourage students to take risks by “assigning competence,” or identifying and naming students’ specific contributions. The vignettes in our book demonstrate many different ways that teachers advance the mathematical agenda of a discussion by strategically highlighting a student’s insight or contribution, especially when a student might not be feeling confident about his or her standing with the rest of the class.
Principle 4: Teachers Must Communicate That All Students Are Sense Makers and That Their Thinking Is Valued
Our last principle is also the most important principle to put into action, because children have to be willing to take risks and put their ideas out there.
Discussions obviously open up the possibilities that students will share their partial and incorrect understandings. How we as teachers respond to errors and partially developed ideas sends important messages about taking risks. It is not easy for students to express their ideas if there is a high burden to be correct and understand everything the first time around.
We need to remember that there’s always a logic behind why students think the way they do, even if they seem off base. We also need to recognize publicly students’ ideas, making sure we don’t single out just a few students as mathematically “smart.”
There are many ways to be smart in mathematics, including making connections across ideas, representing problems, working with models, figuring out faulty solutions, finding patterns, making conjectures, persisting with challenging problems, working through errors, and searching for efficient solutions (Featherstone et al. 2011). Being smart in mathematics is not just about speed and accuracy.
Vivian Paley writes that being curious about children’s ideas signals to them that they are respected: “What are these ideas that I have that are so interesting to the teacher? I must be somebody with good ideas” (1986, 127). We want all students in the class to regard themselves as mathematical thinkers and to see themselves as people who can grow and be successful.
Read more to see the 4 principles applied
Want to see the four principles in action? Download this PDF and you’ll be able to eavesdrop as Ms. Lind moderates a discussion with her class, using an open strategy share and two types of targeted discussions. Student work included!
Elham Kazemi is a professor and associate dean of professional learning at the University of Washington Seattle, where her focus is elementary mathematics education and school-based professional development. In 2012, Kazemi was nominated for the university’s faculty award for Distinguished Contribution to Lifelong Learning. She is a frequent presenter at national conferences.
Allison Hintz is an assistant professor of mathematics education at the University of Washington Bothell. As an elementary teacher, Hintz participated in the Developing Mathematical Ideas professional development.