More Ideas to Spark Mathematical Creativity

Most of us grew up learning math by memorizing facts and practicing procedures—hardly a creative experience!
However, in her book, Mathematical Mindsets, Jo Boaler demonstrates that math is much more about exploring patterns and relationships than following rules, a perspective that opens a space for mathematical creativity.
Spend some time looking at this image. What might you and your students notice and wonder? Give yourself plenty of time to ponder before reading further.
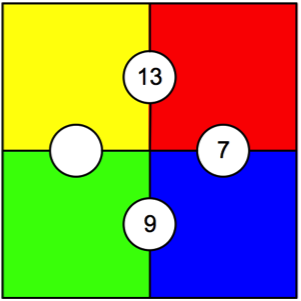
Our brains seek patterns
I was inspired to create this image by a related picture in Sunil Singh’s recent post, The Greatest K to 12 Math Problem Ever. He initially presented his image without directions, allowing the brain to create its own interpretations by doing what it does best—searching for patterns and relationships.
In this important sense, we are all natural mathematicians. Exploring math creatively through patterns allows us to employ talents that we all possess! While we may not always recognize these talents in ourselves, they are often easy to see in toddlers who have not yet accumulated distracting cultural ideas about what math is supposed to be.
The brain’s tenacity in searching for patterns may even lead us astray at times. For instance, it might prompt us to attach unwarranted meaning to coincidences. Or in the math classroom, students, as they work to understand new concepts, may see different patterns than teachers have in mind.
For example, some students believe that 0.19 > 0.2 because they have generalized a useful pattern about whole numbers—that longer numerals (more digits) correspond to larger numbers. Though their conclusion is false, it comes from something positive—their brain’s active and creative attempt to make sense of a new situation by connecting it to earlier learning. Recognizing how the brain works always leaves me feeling more respectful of my students’ thinking!
In a recent post about mindset, “Crazy Math Teacher Lady” Lisa Bejarano suggests that we do not treat such ideas as mistakes but as a natural part of the process of building understanding. In her words, we must “support students in making revisions to their thinking, build from their strengths and enable them the time and support to believe in their own brilliance.” Learning itself is a creative process!
What can we create?
If the notion of mathematical creativity still seems a bit abstract, consider a few concrete possibilities. An open-ended image might lead you to create many of the following:

If you would like to try your hand with a few more images, take a look at these.
Take a look in your teacher’s manual. Do you see anything that might make a great Creative Math Prompt? As you gain experience, you may learn to discover or create your own images!
Zeroing in on concepts and the curriculum
The “anything can happen” aspect of these pictures makes a lot of room for creativity, but in the classroom, you usually need to zero in on particular concepts. Take a look at my collection of Creative Math Prompts. Each of these images can be a seed for a mathematical conversation, task, or investigation targeted to specific learning goals. However, by omitting the written directions, you create new opportunities:
- Make your students’ ideas visible from the start.
- Remove written language as a barrier to understanding.
- Partner with your students in creating the task.
- Facilitate differentiation (because tasks evolve naturally from students’ observations and questions).
Much of my own teaching experience has been in working with students formally or informally identified as gifted. With these students, Creative Math Prompts offer two additional benefits: (1) a practical, meaningful alternative to rushing them through the curriculum (often in a superficial way), and (2) an opportunity to discover and develop talents in students whose abilities are not made visible by traditional identification methods.
Now, if you have been waiting for me to tell you what the image at the beginning of this post is really about, you have been very patient! Of course, it could be many things—any one of them as correct as another.
My ideas are a little different from what Sunil Singh intended when he created his image, and depending on your style of thinking or the age group that you teach, your thoughts will be different from mine. Keep this in mind as you read my comments on the image at my website! For more perspectives on Creative Math Prompts, I invite you to read an earlier MiddleWeb article of mine, How Open-Ended Math Problems Keep on Giving.
Valuing Students’ Ideas
Since “discovering” this image, I have been using it in my professional development work with teachers. At one of these sessions, a first-grade teacher who was excited about her thoughts around the image expressed hurt that I had acknowledged others’ ideas and did not hear hers. I realized that I had become so focused on moving the discussion toward my own preconceived ideas that I had neglected to bring her into the conversation!
The experience reminded me of how challenging it is to truly hear students’ voices, especially when you have standards and learning goals to deal with. Fortunately, this teacher’s choice to express her feelings created a perfect opportunity for all of us to explore strategies for managing this challenge.
Hearing everyone’s ideas can be a slow process. When time becomes an issue, consider having students write down what they notice and wonder so that you can read and respond to their ideas individually. Often, you will be lucky, and students will eventually ask the questions that you have in mind anyway. At other times, their thoughts will lead to valuable discussions and tasks that you would never have thought of!
Remember, too, that time spent early developing a strong conceptual foundation pays off in more efficient use of your time later as students are better able to retain knowledge and transfer it to support new learning.
Modifying images and scaffolding learning
Teachers’ responses to the image at the beginning of this article have given me many ideas for modifying it. Can you see purposes that these modifications might serve? Can you think of other ways to modify the original image in order to focus on particular students or learning goals?
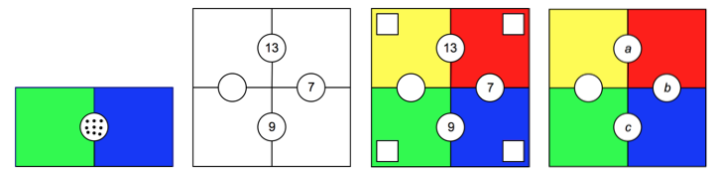
The use of open-ended, visual tasks is a very different way of teaching and learning math than most of us experienced, but its potential for expanding students’ mathematical creativity and understanding makes it exciting and well worth exploring!
Resources
► See more of Jerry’s ideas for sparking math creativity in this earlier MiddleWeb post.
ALSO SEE:
Creative Math Prompts, by Jerry Burkhart, contains a large set of images like the ones described in this article.
Intrepid Math, by Jerry Burkhart, is a collection of challenging, open-ended problems for students in grades 4–6.
Deep Math Projects (early to middle elementary) and Deep Algebra Projects (middle school to high school), by Jerry Burkhart, are rich, complex mathematical and real-world investigations that stretch advanced learners out of their comfort zones.
Extending the Challenge in Mathematics, by Linda Jensen Sheffield, contains an excellent collection of open-ended math activities to challenge promising math learners in grades K–8. One of the activities, Field of Dreams, uses images like the one the beginning of this article.
Good Questions: Great Ways to Differentiate Mathematics Instruction in Standards-Based Classroom, by Marian Small, describes open questions and parallel tasks as vehicles to differentiate for the needs of all math learners.

As founder of 5280 Math Education, he helps schools and districts implement research-based programming for gifted math students and offers tools and strategies for developing and nurturing adventurous math learners. Visit his store at MyEdExpert. And read more of his articles here at MiddleWeb.

































