Math Play with Patterns and Relationships
 By Jerry Burkhart
By Jerry Burkhart
Are you looking for fresh ideas to enliven your math classes in the new school year? How about spending more time playing with math concepts?
Dr. Eugenia Cheng, whose work I referred to in an earlier MiddleWeb post about collaboration and competition in math (one of her aims is to “rid the world of math phobia”), recently gave a presentation that inspired me to think in new ways about mathematical patterns and how they connect to creativity and play in math.
I was surprised to hear Dr. Cheng say that she is not especially fond of mathematical games and problems. Her interests lie more in creating, representing, and communicating mathematical ideas. I was especially struck by her use of diagrams to make abstract math concepts more approachable and meaningful.
While Cheng tends to talk and write primarily about advanced ideas related to her own work as a mathematician, I have found that the diagrams she discusses apply equally well to elementary and middle school math.
Beginning to play
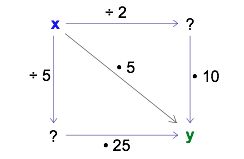
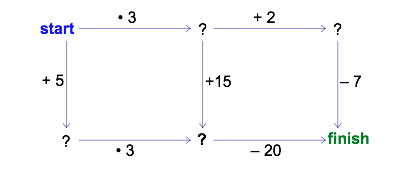
What do you see in the following diagram? How could you play around with it? (The dots before the 10 and the 25 represent multiplication.).
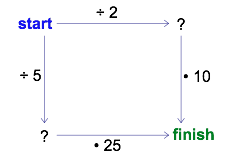
Because there are no numbers in the ‘start’ and ‘finish’ corners, you may choose your own. Try it! Pick a ‘start’ number and follow the arrows to the ‘finish.’ As you travel, carry out the action shown on each arrow. You might get something like the following diagram.
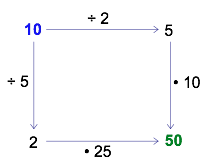
Though it may feel strange at first to work without having concrete instructions, doing so is the essence of mathematical play! Most of us have been trained to be ‘rule followers’ in math. Working without instructions encourages us to be more creative and observant.
Patterns and relationships
If you pay close attention as you continue to choose a variety of ‘start’ numbers, you may begin to notice some patterns.
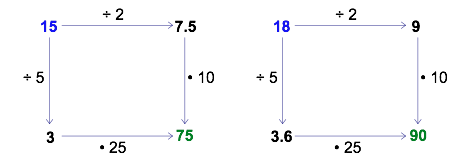
It appears that the ‘finish’ number is always the same regardless of whether you follow the arrows to the right and then down or in the opposite order, down and then to the right. Furthermore, the finish number always seems to be 5 times greater than the ‘start’ number. You might even imagine a “shortcut” path straight from start to finish.
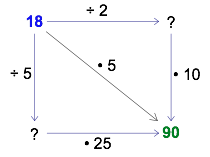
Diagrams like these expand students’ focus beyond isolated calculations to the patterns and relationships between them.
Making connections to algebra
Because the patterns above hold for every possible ‘start’ number, you may also describe them using variables.
Each path from start to finish represents an equation.
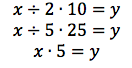
All three expressions are equivalent, because they lead to the same result regardless of the value you choose for. Thus, the diagram illustrates the relationships:
![]()
Finding new patterns by modifying diagrams
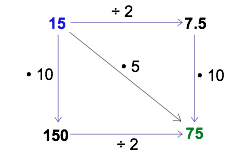
You may discover even deeper patterns by creating your own actions along the arrows. For example, suppose you make both pairs of arrows have the same operations but in a different order. The following diagram seems to suggest that it does not matter whether you do the multiplication or the division first. Is this true for all ‘start’ numbers? Is it true if you use other numbers in place of 2 and 10? Play around with the diagram and find out!
Another option is to look for more combinations of actions that cause the ‘finish’ number to be 5 times greater than the ‘start’ number. For example:
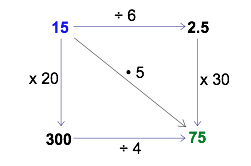
After doing this for a while, you may discover that (to maintain the shortcut path) the number you multiply by must be 5 times greater than the number you divide by. For example, 30 is 5 times greater than 6, and 20 is 5 times greater than 4.
Once you notice this pattern, new questions follow quickly. Why does this pattern make sense? How can you create other relationships between the ‘start’ and ‘finish’ numbers (for example, making the ‘finish’ number one-third as large as the ‘start’ number)? How can you use variables to represent the new patterns?
More connections and questions
Our explorations so far are just the tip of the iceberg! There are many more ways to play with the diagrams. Here are just a few possibilities (you might use these to differentiate challenges).
- Include fractions in the diagrams. Do the patterns change?
- Use addition and subtraction in the diagrams. Compare and contrast them to the multiplication/division diagrams.
- Include negative numbers in the diagrams. Do earlier patterns still apply?
- Try combining addition and multiplication in the same diagram. Is it still possible to create shortcut paths? (This may lead to discussions of the distributive property.)
- What happens if you try to run some of the arrows in reverse?
Question 5 shows the power of the diagrams to help you discover new relationships from old ones. For example, suppose that you simply reverse just the top arrow in one of our earlier diagrams.
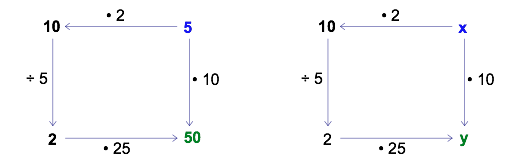
When you reverse the top arrow, the division by 2 turns into multiplication. Additionally, the start and finish numbers are now both on the right side of the diagram (can you see why?). If you follow the arrows carefully, the resulting diagram suggests a new algebraic relationship.
![]() Imagine the new relationships that students can discover by playing with reversing arrows in different diagrams! (Note: Reversing the arrows may not always make sense – for example, when dealing with squares, square roots, and negative numbers).
Imagine the new relationships that students can discover by playing with reversing arrows in different diagrams! (Note: Reversing the arrows may not always make sense – for example, when dealing with squares, square roots, and negative numbers).
Other kinds of diagrams
All of our diagrams so far have been commutative, meaning that you can ‘commute’ (travel) from start to finish by different routes without affecting the final result. It is important to understand, however, that not all diagrams are commutative!
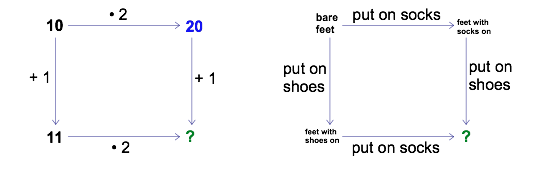
Diagrams like these create fun new opportunities to connect patterns in math to everyday experience.
Suppose that instead of using arrows to represent actions or operations on numbers, you use segments to represent some relationship between the numbers.
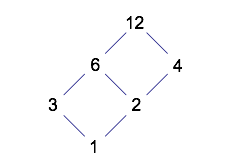
In this diagram, numbers that are joined by a segment have a factor/multiple relationship. A number is a factor of a number above it if and only if you can follow a downward path from the upper to the lower number. (For example, 3 is not a factor of 4, because you would have to travel upward along a segment at some point in order to get from 4 to 3.)
The structure of the diagram for 18 is the same as for 12. Spend some time looking at all of the beautiful patterns in these diagrams!
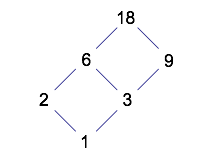
The structure for 30 is quite different. In order to show the relationships correctly, the diagram takes on a three-dimensional appearance.
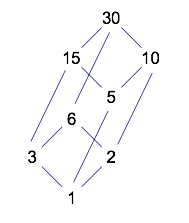
The diagram for 42 has the same structure as the one for 30. Try to create it!
Again, there is a lot of room to play around with diagrams like these. What numbers have diagrams with a structure like the one for 12 and 18? What other kinds of structures can occur for different numbers? What causes the similarities and differences in the structures? Can you predict the structures before drawing the diagrams?
As a striking and thought-provoking example of the ways in which mathematical patterns can mirror and describe real-world relationships in unexpected ways, Dr. Cheng has created a diagram like the one above to represent power relationships between groups of people.
Summary
Diagrams that show relationships between operations and numbers create engaging and meaningful opportunities for students to play with mathematical concepts. I hope that you enjoy playing with the examples I have shown and that they inspire you and your students to create and explore your own visualizations.
I will close with a final example that suggests the possibility of building new diagrams by joining smaller ones. Have fun playing with it and creating your own!
Resources
How to Bake π: An edible Exploration of the Mathematics of Mathematics, by Eugenia Cheng
A fascinating book by Dr. Cheng that includes a number of ideas that inspired this article and much more, including many connections to everyday contexts (especially baking!).
Creative Math Prompts, by Jerry Burkhart
Simple images designed inspire mathematical creativity and deep thinking for early, middle and later grades. Free at my website!
 Jerry Burkhart is a mathematics educator and consultant with over 30 years of classroom experience. He is the author of the book series, Advanced Common Core Math Explorations, published by Prufrock Press, and he presents regularly at state, regional, and national conferences on topics related to mathematical talent development.
Jerry Burkhart is a mathematics educator and consultant with over 30 years of classroom experience. He is the author of the book series, Advanced Common Core Math Explorations, published by Prufrock Press, and he presents regularly at state, regional, and national conferences on topics related to mathematical talent development.
As founder of 5280 Math Education, he helps schools and districts implement research-based programming for gifted math students and offers tools and strategies for developing and nurturing adventurous math learners. Visit his store at MyEdExpert. And read more of his articles here at MiddleWeb.



































Fascinating and useful! Thank you.