Math: Is Test Correction a Good Use of Time?
A MiddleWeb Blog
 The students have taken the test. I’ve graded it. Now what?
The students have taken the test. I’ve graded it. Now what?
Recently my Algebra II with Trig classes took a test on exponential functions. They struggled with certain parts of the test, and I decided to allow them to make test corrections to earn extra points.
In my class, test corrections involve students reworking the test problems that they missed, my regrading their work, and the students receiving extra points to add to their test grade.
Every time we do test corrections I wonder if it does any good. The students want to make the corrections to get extra points, but does it help them master the concept?
Test correction is an area where I haven’t made much improvement since my first years of teaching. Except for a few minor tweaks, my students are doing test corrections much the same way my classes always have. And every year I think, “there has to be a better way.”
What I Want to Accomplish
I allow students to make corrections after the test because I want students to realize that taking a test does not close the door on that concept. In math, it’s always “better late than never.”
Also, I realize that some students suffer from stress when they take a test, and test corrections allow them to have a second look at the problems, minus some of the test anxiety. Many students have told me that most of their errors come from simple math mistakes as a result of nerves.
I also want students to take the time to reflect on the problems they missed so that they discover why they missed the problem. Was it a math error, failure to the read the instructions, or a failure to understand the concept?
Finally, test corrections give me information that I wouldn’t otherwise have. If a student can explain why they made a certain mistake, I can use that information to help that student and other students as well.
What Actually Happened
As I mentioned, my students recently made corrections to the test covering exponential functions. The students were eager to correct their mistakes but were preoccupied with how much additional credit they would receive. “How many points will I get for this?” is something I heard over and over.
I did not give the students a template to work from, which I usually do. I did require that they complete the corrections on a separate piece of paper. I instructed students to explain their thinking and show all their work. They could use the notes we took in class, watch video tutorials, or ask me or other students for help. I did not assign students to a partner, although they could work together if they chose.
I walked around the room to ensure that students were collaborating, not copying from each other. When students asked how much credit they would get back, I told them extra credit would be based on the quality of their work.
I took my time reading their test corrections. I really tried to understand why the students missed the problem and also what part of the problem they got right.
I found this scrutiny to be time well spent. It helped me see that a lot of students understood exponential functions but were having trouble solving equations! I probably wouldn’t have caught this if I hadn’t gone through their tests again.
As far as the quality of work, some students did a great job while others just wrote something down. Some of the test “corrections” were still incorrect. You could tell some students were interested in letting me know why they had missed the problem, and others were just writing something down because they wanted extra points.
It became clear as I looked through their papers that I need to make some adjustments and do a better job of helping students know how to correct their work and assess their understanding. For starters, I decided to ask my students a few questions regarding test corrections to gauge their opinion on the matter and see if they had any suggestions.
What Students Think About Correcting
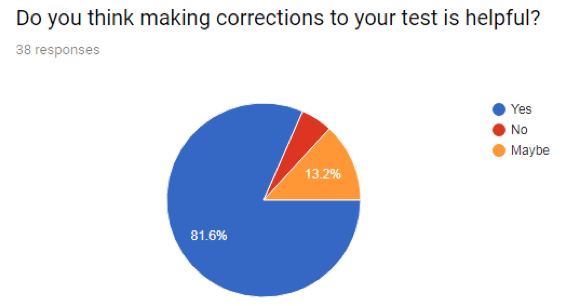
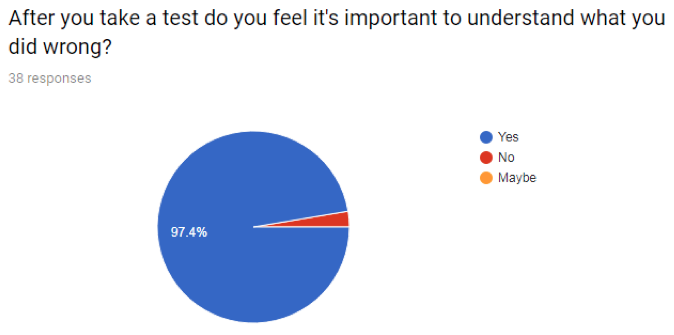
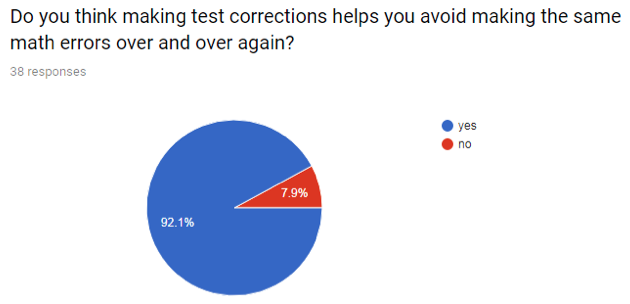
I was surprised with students’ overwhelming endorsement of test corrections. Almost eighty-two percent thought the process was helpful (Question 1), and ninety-seven percent felt like it’s important after a test to understand their mistakes (Question 2). When I asked if correcting their tests would help them avoid making the same errors in the future (Question 3), almost everyone said yes.
My biggest eye-opener
The biggest surprise to me was the way students responded when asked an open-ended question: How can I best help you after a test? Many students said they would benefit by talking one on one with me and having the opportunity to discuss what they missed.
Students responded with comments like “I want to explain in person” or “I want you to explain to me how I missed the question.” I hadn’t thought of this before. I’ve had informal post-test discussions with students in the past, but having a conversation was never a deliberate part of my test corrections process.
After reading these responses, during our next round of test corrections I made a point to invite some students to talk with me one on one. The students spoke very thoughtfully about the mistakes they had made and how to prevent making them in the future.
This is probably the first time I’ve come close to getting the amount of thought and reflection I’ve always wanted from the test corrections process.
My Plan for Improvement
After much thought and discussion with my students, I’ve decided on a few changes in how I handle test corrections:
- I’ll allow adequate time for students to correct their tests and to reflect on their learning.
- I’ll provide students an opportunity to discuss their thinking with me one on one.
- I’ll make a short list of “take-aways” as I review test corrections to use as a reference next year. (For example, a “take-away” could be a common mistake made by students or a test question that needs to be modified or removed.)
- I’ll start at the beginning of the year demonstrating the quality of work that I expect when they do their test corrections.
I know this is just a beginning and I’m not exactly sure how this is going to look in my classroom. I hope in the not too distant future I’ll be able to provide an update. Meanwhile, if any readers have any suggestions, I would be very grateful!
































The feedback from students supports that they are learning from their mistakes, a big part of a growth mindset. This is something for them to realize. My personal experience is that when I make a mistake I learn from that. Jo Boaler would say that your brain learns best when making mistakes, even better than when you get them correct. Struggle and expending energy to learn are important for students to recognize. One strategy that I use is to take some questions from the first test that the students had problems with and put them on the next test. Students realize that once the test is over they still need to learn the material. When taking a quiz or test have the students indicate for each question a C, S, or R for their feelings about the question. C = confident, S = Shaky or R = reteach please. Questions are identified by topic and students indicate if the question was right or wrong. Then they indicate was a simple mistake, they got lucky, or they don’t get it. http://hechingerreport.org/getting-errors-all-wrong/ talks about learning from mistakes.
Thanks for the idea about C, S, and R. I have my students tell me how they felt before the assessment and after the assessment, but I may start using your method. Thanks again.
Thank you for the great information! I love the C,S,R suggestion. I’m doing that on our next test!
I love your ideas and the way you analyzed your data. Making corrections on any assessment is crucial. The person who does the editing or correcting is the one doing the learning. So, I have my students do corrections all the time – on everything, including homework. I give points back on homework, but do not give points back on quizzes and tests. For middle school students, I do allow retakes on tests with a new test after they do all of their corrections correctly. And if I give a quiz and then a test, I have them correct the quiz. If they score higher on the test, I change their quiz score to reflect the learned skill. I do not give extra credit because I want them to learn the skills they need to learn.
Wow! That is a really good idea! It never occurred to me to go back and change the quiz grade. Great suggestion! Thanks!!
I have always had one on one discussions on correcting test items after testing in math and reading. When I taught math my students had to go back and correct their wrong answers. This has been such a game changer for me as a teacher. Students are personally accountable for the work that they put in to their assessments, and they can see where they need to ask more questions or focus on themselves. We spend quality time going over the questions and coding or recoding the text so that the evidence is precisely clear. When students walk away they know that the answer is in the text whether explicitly there or as an inference.
I also love your idea of C, S, and R. I will use this method the next time we assess. I do ask my students what they thought about the assessment before and after the test. This also gives accountability.
Thank you for your comment! I liked what you said about students reflecting after the test and realizing that maybe they should have asked more questions. Like you said students need to know they “are personally accountable for the work they put in their assessments.”
Thank you for this article. I think this is a great idea. I offer test corrections (where students can earn back up to half the points they lost). Students have to explain what they did incorrectly the first time, explain the correct solution, and explain how they could prevent their errors in the future. I think having a discussion would be better than having the students write all of this information down. I think it would be difficult for me to find the time, but as teachers, we always find a way to make things happen! Thanks for the insight and tips!
Thanks for your comment! I’m like you, I’m not sure how I’m going to find the time to talk with my students. I will say that after this last test I gave, not every student wanted or needed to talk with me one on one. I think there are some that can communicate better verbally than trying to write it down. -I also let my students earn up to half the points they lost.
I am enjoying the discussion. Here are a couple of other resources for mistakes. Here are two videos by the same person about “My favorite No”
https://www.teachingchannel.org/videos/math-test-grading-tips
https://www.youtube.com/watch?v=srJWx7P6uLE
This is a form for after the test similar to C,S,R
https://docs.google.com/document/d/1KPLUzcLc_NnRqbmQcUJo3xE7JZQlHr4l1p1ChmpVb7k/edit?usp=sharing
I like the form you shared. That would be a quick way for my students to analyze the results from their benchmarks, I could use Google docs and then I would have access to all the data. Thanks!
I also have the students do a SAID analysis S=simple (usually sign) mistake, A=algebra mistake, I=I didn’t know how to do the problem (actual concepts being assessed), D=Directions threw me off or I didn’t know what the directions were asking me to do. Then I have them keep a running list of their repeated mistakes by category so they know if they need to focus on repeatedly missing signs or misunderstanding directions. It has really helped the students help themselves!
That is a great idea! Simple and straightforward, and so helpful! It would be good for the students to see what kind of mistakes they were making and it would help me too. If a lot of the students put D (directions) I would know I needed to go back and improve my directions. Thanks!!
I do something really close to what Paige Weir suggests. All mistakes are categorized based on calculation errors, sloppiness (misaligned numbers , miscopying, etc), directions, incorrect set-up or misunderstanding a concept. This also helps to see if there is more than one type of error in the problems missed or if there is a pattern to the types of mistakes made. This can really help to provide more specific focus for what to remedy and how. Bravo for all of the input here!
I let kids who scored below 80% correct their quizzes/tests and gain back full points so they can improve their score up to a max of 80%. The rationale is that maybe the didn’t prepare as well as they should have, so they shouldn’t have a shot at higher than and 80. I have done this on chapter quizzes and the chapter summative test. However, I am starting to wonder if this opportunity creates a defacto ‘safety net’ mindset with *some* students such that they don’t prepare as well, in reliance upon the self-correction process. I administer self-correction under testing conditions: it usually happens the day after the assessment, and after our new lesson, at the end of class when they might normally work on practice problems or begin homework. I will also step aside with individual students and prompt them as minimally as I can to see their trouble spots with their incorrect work, often with no words said, though I will pose guiding questions with problems. In the end, they must use a different color pencil to correct their work, or circle the problem with a highlighter or something to draw my attention to the new work. It’s more work for me to do this ‘re-correcting’, but, it saves so many students. Next year, I’m considering self correction on quizzes only, and you get what you get on chapter tests. This is to ratchet up the accountability for the summative, as well as raise the stakes for their preparation efforts, and thus better learning/retention (hopefully) from the quizzes. We’ll see.
My school [American School of Bombay] makes us make correction to math tests, they are called supercorrections. My school uses 1-7 grading system. If you got a 1, 2, or 3 on the test, if you do your supercorrections well, your grade increases to 4. If you have a 4 or 5, your grade increases by 1. You cannot supercorrect if you have a 6 or 7. We have a form with the sections, one to explain the errors, and the second to redo the problem correctly. We must do this for any problem we got wrong.