How I Learned to Love Middle School Geometry

By Christopher Danielson

I need to tell you a secret. I used to hate teaching geometry.

The hierarchy of quadrilaterals was a formality that answered no questions my students ever wondered about. I (and consequently, my students) saw proof writing as a tedious exercise in stiffly demonstrating what my students already took to be true, and what they didn’t seem to care very much about. Geometry diagrams had their own secret code my students struggled to crack.

Geometry – in my former way of viewing it – had too much vocabulary, too much formality, too many rules.

But I am writing at this moment to tell you that I have changed, and I want to share some tools that have fostered this change.

I now see geometry as a playground of ideas for students of all ages. Geometry now presents opportunities for exploration, wonder, and delight in my teaching. Here is my story.

The hierarchy of hexagons

A few years back, I wondered whether my aversion to the hierarchy of quadrilaterals might be that it is completely determined already. I began to wonder whether having students participate in developing a new hierarchy might be a more interesting task.

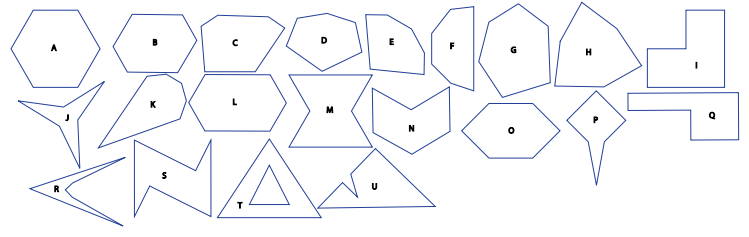
But students already know a lot about quadrilaterals, so I needed something fresh. I developed the hierarchy of hexagons.

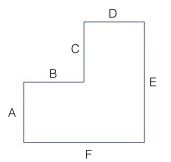
I offered my students about 20 widely varying hexagons. We noticed properties of these hexagons, and we used these properties to define classes of hexagons. For instance, one class defined a Utah (i) as a hexagon with all right angles.

As we explored other shapes and properties, the relationships and questions began to put pressure on our previous understandings. In particular, once we had a good working definition of concave as being about having angles greater than 180°, it became clear that Utahs really don’t have all right angles – one of those angles measures 270°.

Suddenly, vocabulary came alive in my geometry classroom. We needed a word to describe the 270° angle, and that would distinguish it from the 90° angle we had previously paid attention to. We needed the term interior angle; it described the precise thing we were struggling with.

What is more, putting this term in the mix enabled us to ask a whole bunch of new questions. Is it possible for a hexagon to have six right interior angles? A Utah has five right interior angles; can a hexagon have five acute angles? What is the difference between not being able to think of examples of hexagons with these properties and being certain that they don’t exist?

These student questions were wholly original

These are not questions whose answers are to be derived from a set of givens in a textbook. They do not lead to a pre-existing hierarchy we can look up on the internet. Indeed, I didn’t have an answer key to refer to because the questions were wholly original and arose from my students’ minds as we explored this rich set of constraints together.

Finally, we began to organize our classes of hexagons into a hierarchy. This led to questions like, “Is there such a thing as an equilateral Utah?” My students began to argue that sides A and C together add to the length of side E, and that means C has to be shorter than E, and this is true for every Utah that could ever be. In short, they proved a theorem.

This exploration took place in my college math course for future elementary, special education and middle school teachers, but the mathematics would have been exactly right in my former middle school classroom.

The hierarchy of hexagons opened my eyes to the potential of geometry for creating rich, interesting, and challenging mathematical experiences for students. I soon began to look for other opportunities to open conversation about geometry in classrooms of widely varying grades, and in children’s homes.

Building a better shapes book

Being a parent, I knew first hand that the world needed a better shapes book than most children encounter. Most shapes books have separate pages for squares and for rectangles (and then we wonder why 7th graders cling so tightly to the idea that squares are not rectangles). They leave little for children and parents to discuss or to think about after reading.

This stands in stark contrast to the rich narratives offered to young children in story books. A four-year-old can laugh along with Frances as she sings songs about jiggly eggs, bread, and jam, and then discovers the delights of a varied diet.

Children can connect such stories to their own lives, and use them as touchstones for understanding their relationships to the world and to other people. Yet the shapes books they encounter inform them that rectangles have two short sides and two long sides, which is both false and uninteresting.

This desire for a better shapes book mixed with my newfound wonder at the power of geometry for opening up possibilities. Then some colleagues’ adaptation of an old Sesame Street segment provided the format for bringing these ideas to life, and my book Which One Doesn’t Belong? was born.

In the original Sesame Street format, there are three things that are the same, and one that is different. “Which one of these things is not like the others?” is a question with one right answer.

My math education colleagues Terry Wyberg and Megan Franke breathed new life into the format by creating sets where each of the four objects had a reason not to belong. They worked mostly with numbers. I applied the idea to shapes, and developed the book as a series of which one doesn’t belong? prompts that develops in complexity and richness, and that invites readers to explore many important corners of the world of geometry.

The sets share two key characteristics

The book starts simply, with a page that provides everyone an opportunity to participate without needing a sophisticated geometric eye. Students at all levels attend to shading, orientation, composition and decomposition of shapes, numbers of sides and vertices on the opening page.

The sets become more complicated fairly quickly, but they share two important characteristics:

1. Any shape on any page can be seen as different, with the others having something in common, and
2. There are multiple ways to distinguish any shape.

“Which one doesn’t belong?” has more than one right answer, and each answer has more than one reason. The measure of what is right is what’s true, not what’s in the answer key.

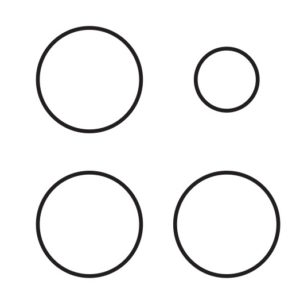
When students consider a set of shapes that generally don’t appear in geometry textbooks, such as those in the figure below, they begin to ask questions that don’t appear there either.

• Does a heart have vertices?
• Is something a “shape” if I don’t have a name for it?
• How can we measure an angle where two curvy sides come together?

These questions get to the heart of what it means to do mathematics. They arise in classrooms of all ages, where students can address them with varying levels of rigor and sophistication appropriate to students’ ages.

Middle schoolers love to test boundaries

Middle school students need to build informal arguments in preparation for the more formal proof work in high school. But more importantly, middle schoolers need to build arguments because this is what they do. Early adolescence requires finding and testing the boundaries that have constrained their intellectual and social worlds.

Perhaps – like me – you haven’t previously seen geometry as a natural place for this developmentally essential exploration to occur. I hope my story has given you hope that it is, or has confirmed what you know in your teacher heart to be true. Either way, I encourage you to dig deeper. Here are some resources for continuing the exploration with your students, and for your own learning.

You can find lots more of my writing in two books: the bundled Which One Doesn’t Belong? A Shapes Book and Teacher Guide and Common Core Math for Parents for Dummies. Also check out my blogs: Talking Math with Your Kids and Overthinking My Teaching.

More Which One Doesn’t Belong? prompts are available at my Stenhouse website, and at wodb.ca. Additionally, you’ll find prompts and discussion on Twitter by searching the #wodb hashtag.

____________

Christopher Danielson has worked with math learners of all ages, from teens in his former middle school classroom to his own children, from calculus students to elementary teachers to families who visit his Math On-A-Stick learning space at the Minnesota State Fair. Find more of his writing on his websites, talkingmathwithkids.com and christopherdanielson.wordpress.com.