Stop Using These Four Words in Math Class
By Dan Ilaria

Feeling some word exhaustion is normal because it turns out language learning and mathematical learning depend on each other.
According to Stanford’s Center for Assessment, Learning and Equity, mathematical language needs to be developed along with mathematical sense making. So writing down vocabulary definitions without the opportunity to explore and play with ideas first doesn’t advance learning.
Also, students can be confused by mathematical words or phrases with broad or multiple meanings, and this can create unnecessary frustration and stress when learning new concepts.
Let’s review four words or phrases teachers should eliminate from their classrooms to help reduce confusion, stress, and anxiety.
Bad Word: Cancel
Imagine teaching a student to solve 3x = 9. You might say “cancel the three” to get the answer, x = 3. If solving x + 3 = 9, you might also say “cancel the three.” However, the student will need to do two different operations to solve the equations. Confusion.
The word cancel is also commonly used for combining like terms or dividing common factors. That isn’t really what you’re teaching students to do in these examples. Using this word can cause confusion, especially when you’re using it in various ways.
What should we do instead? The teacher should name the mathematics they are doing. This is a way to engage in the mathematical practice “Attend to Precision.” To break the habit of using cancel, teachers should take the time to name the mathematical operations being performed and help students focus on the goal of their work.
For example, if a student is solving 3x = 9, the teacher would explain they divide both sides of the equation by 3 because they want the coefficient of x to be 1. By naming the mathematical operation, students get a better understanding of their work, instead of getting confused by what it means to “cancel” in that specific situation.
 Bad Word: Plug in
Bad Word: Plug in
When teachers and students are saying, “plug in,” this phrase is often used in various ways with different meanings. A teacher could ask, “when solving an equation, how do you check your answer?” or “when solving a system of equations for x, how do you find y?” and the student would answer, “plug in my answer,” or “plug in x.” This phrase can easily cause confusion since there is no “plug in” property of equality and “plug in” is an everyday phrase.
Instead, teachers should explain how students are using the substitution property of equality. Using this concept in the classroom helps students understand what they are doing and uses proper mathematical language.
For example, students are finding the value of the expression 8x + 3, when x = 6. The substitution property of equality states that if a = b then b can be substituted in for a, so students know to substitute 6 for x to evaluate the expression. There is no “plugging in” happening in this problem – leave the plugging in for charging phones and tangled up computer cords!
Bad Word: Reduce
A teacher writes the fraction 9/6 on the board and tells students to “reduce” the fraction. Students can come up with the answers 6/4 or 3/2; however, did the value of the fraction really get smaller? No, so why are we asking students to reduce the fraction?
All of these fractions equal the same value, yet we often tell students to reduce the fraction which would be making it smaller. This can easily cause confusion for a student when they are looking at the three fractions equaling the same thing, yet hearing the teacher explain the fractions as “reduced.”
Instead, for these types of exercises teachers should have students “rewrite the fraction in an equivalent form.” Students would then write 9/6 = 6/4 = 3/2. They’re rewriting the fraction, while also understanding all of the fractions have the same value.
Bad Word: Cross-multiply
Just like the first three words and phrases, “cross-multiply” is another phrase that causes unnecessary confusion among students. Students are often told to cross-multiply to solve equations like this one:
x/9 = 2/3
However, cross-multiplication creates common errors for students. Once introduced, cross-multiplying leads to confusion and frustration because when many students see two fractions, they want to cross-multiply. One common place this happens is with adding fractions. Students learn to cross-multiply to find common denominators rather than make sense of how addition and subtraction requires fractions having the same size.
In the Building Concepts series of activities from TI Education, there are opportunities for students to explore fractions dynamically. The screenshots show how a student adding 1/2 + 1/3 can change the size of the fractions to create two new equivalent fractions with the same denominator. This allows students to make sense of the operation before learning shortcuts that could be applied incorrectly later.
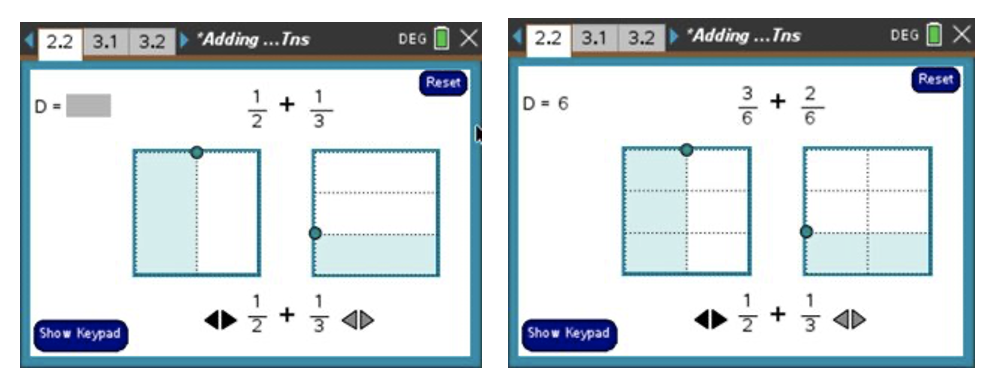
Instead of cross-multiplying when solving proportions, it’s important to note a proportional relationship is a collection of pairs of numbers that are in equivalent ratios, as stated in the Common Core Progressions Documents When we write an equation, we are setting the value of two ratios equal to each other. So, we can think of the relationship as equivalent fractions or as solving an equation.
Returning to x/9 = 2/3, if we see equivalent fractions, we see the denominator is multiplied by three from 3 to 9, so our numerator must be multiplied by 3, which tells us x = 6. If you see the equation and think about how to solve it, we can just multiply by 9 on each side of the equation to find the value of x. Both processes are fewer steps than the cross-multiplying algorithm.
Take-aways
Stop saying “cancel” and use “name the operation.” Stop saying “plug in” and use “substitute.” Stop saying “reduce” and use “rewrite.” Stop saying “cross-multiply” and allow students to make sense of what they are solving.
Consistently highlighting and amplifying academic language will help students learn, particularly English Language learners. So don’t forget to use proper academic vocabulary so students make sense of mathematics!
Dr. Daniel R. Ilaria is a Professor of Mathematics Education at West Chester University in Pennsylvania where he works with teacher candidates on learning effective pedagogical practices and building pedagogical content knowledge.
He is the Program Coordinator for secondary mathematics education and Project Director for the WW STEM Teaching Fellowship and NSF NOYCE W.I.S.E.R grants. He also helps teachers improve their instructional practice as an instructional coach, a T3 National Instructor, and Illustrative Mathematics Certified Facilitator.
This article is based on Dr. Ilaria’s presentation “Math with Bad Words and Phrases” at the 2023 annual conference of the National Council of Teachers of Mathematics (NCTM).































Can we add carry and borrow to the list also and change them to trade or regroup.