Turn Your Math Class into a Math Community

Instructional coach, curriculum specialist and district math coordinator Gina Picha shows how K-8 teachers can use the tool of conferring to transform math classrooms into math communities.

By Gina Picha

In my first few years of teaching, I used the term community, and specifically math community, to describe my math classrooms. Looking back, I don’t think I put too much thought into what this actually meant or how math communities differed from classrooms of math learners.

The truth is that authentic math communities don’t develop on their own and require intentional planning. This intentional planning is necessary because for many students and teachers this is a new type of learning environment.

Community vs. Classroom

In an authentic math community, students are engaged in mathematics with the goal of understanding and making new discoveries rather than the goal of completing assignments. These learning environments support students in developing the understanding that their ideas are valuable and that their participation in the community is necessary to grow the community’s collective understanding.

One way to facilitate this way of learning mathematics is by having regular math conferences with your students.

---

---

Conferring as a Daily Practice

Math conferences are conversations with students that take place as students are working on math tasks or problems. This time is ideal because it is likely a time that is already part of your math block or class period and a time when students are problem solving in pairs or in groups.

The best way to get started is by sitting beside a group of students and listening in as they grapple with the problem or task and develop and share ideas with one another.

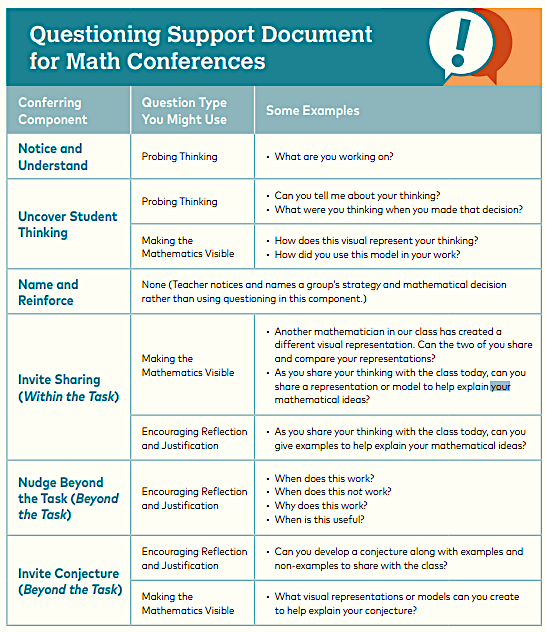
There are two conferring structures that can help to facilitate these conversations so that students are nudged to think deeply about the mathematics, share their ideas, and develop conjectures. These two structures – Conferring Beyond the Task and Conferring Within the Task – differ slightly, and the choice is a decision made after the conference begins.

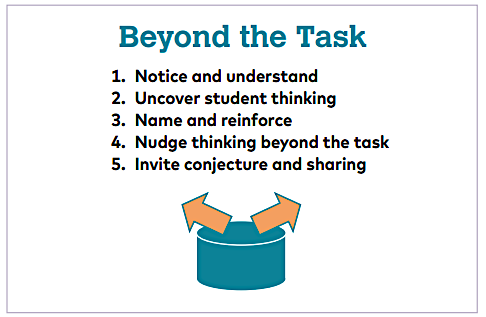
(1) Conferring Beyond the Task

When conferring Beyond the Task, you nudge your students in ways in which their thinking moves from the current problem to developing a broader generalization beyond any one problem and then developing a conjecture to share with the class. This conference has five components:

See if you can spot the components in this example with 6 grade teacher Ms. Davinki and her students, Chase and Bella, who are working on a task involving ratios and proportions.

Ms. Davinki: What are you working on?

Chase: We are trying to figure out which situation would give each person the most food. It says that 3 people could share 2 sub sandwiches or 5 people could share 3 sub sandwiches.

Ms. Davinki: What ideas have you come up with?

Bella: Well, we started by drawing a picture. Then that reminded me that this is like division.

Chase: Yeah, so we decided to think of each situation as division and write them both as fractions. In situation 1, each person gets ⅔ of a sub because that is saying 2 sandwiches divided by 3 people. In the second situation each person gets ⅗.

Bella: So now what?

Chase: Well, we want to know which is more.

Bella: So we need to compare them. I remember how to do this. We can find a common denominator.

Ms. Davinki: It sounds like you are saying that you can use what you know about comparing fractions to compare ratios.  Do you think this works with any ratios that you want to compare?

Bella: I think so.

Ms. Davinksi: Why don’t you work out this problem. If you are right and it works, see if you can come up with some more examples to test this out and form a conjecture. I think our math community would benefit from learning more about how they can use their understanding of division and fractions to compare ratios.

---

---

Nudging students to make conjectures

Did you notice how Ms. Davinksi asked Bella and Chase to think about how their idea about comparing ratios works with problems other than the task they are working on? This decision was made in the moment when Ms. Davinksi decided that Chase and Bella might benefit from thinking about the connections they are making between ratios, fractions and division and additional problems they might consider.

Asking students to make conjectures positions them as capable mathematicians with the important task of figuring out how the mathematics works, developing their own examples, and sharing their findings with the class.

Although developing, testing, and sharing conjectures is an important part of a math community, there may be times when you feel that students would benefit from further exploration of the math within the confines of the current task.

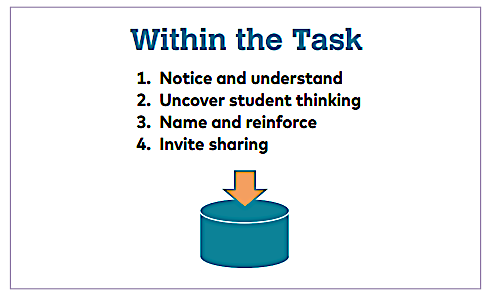
(2) Conferring Within the Task

As you read the following Within the Task conference between 5th grade teacher Mr. Watz and his students, Bailey and Daniel, try to spot the following components:

Mr. Watz: As I was listening in, I noticed that you are using base ten blocks. Can you tell me a little about your thinking?

Bailey: Well, we are stuck.

Mr. Watz: It seems like you got started by using the base ten blocks. What were your thoughts?

Daniel: Well we are trying to solve .50 x .68. So we built .68 by using 6 tens rods and 8 cubes. If the problem said 5 x .68, then I know I could just build this 5 times and then add up the total. But since both numbers are decimals, I am not sure what to do.

Mr. Watz: What are you thinking, Bailey?

Bailey: I don’t know. With whole numbers we could do Daniel’s suggestion, because if it was 5 we would say 5 groups of .68. But now, I guess we could say .5 groups of .68. I don’t know what that means.

Daniel: Well .50 is one half. So maybe we can say one half of .68. Is that right? (Bella begins separating the base ten blocks into two groups of .34.)

Mr. Watz: That is interesting. You thought of the decimal as a fraction in order to make sense of the problem.

Daniel: Is .34 right? Does that make sense? That is smaller than .68.

Mr. Watz: I think you and Bailey have a really interesting way of thinking about this problem. I was just conferring with Taylor and Zaya and they were modeling their ideas by representing the values with colors on a hundreds grid. I am wondering how your ideas and their ideas might be connected. Why don’t you meet with Zaya and Taylor to share and compare your ideas.

Choosing a structure will always be subjective

Mr. Watz began the conference with Daniel and Bailey by listening to their thinking and understanding their ideas about how to find the product of .50 and .68. Mr. Watz made the intentional decision to confer within the task as he believed the boys might gain a deeper understanding of the mathematics with time to make connections between their ideas and the ideas of their peers.

Although Mr. Watz decided  to confer within the task, students may also have benefited from a nudge beyond the task to make a conjecture. Choosing a conference structure will always be a subjective process, and it is important to remember that conferences are conversations. In the moment, you should trust that no matter which structure you choose, the conversation is supporting and nudging your students to dive deeper into the mathematics.

Revisit Ideas with Conjecture Tours

Making and sharing ideas and conjectures are essential parts of an active math community. But what happens to students’ ideas after they are shared? One way to help students revisit their ideas and the ideas of their peers is to post students’ conjectures on the walls of the classroom and have students participate in Conjecture Tours.

Conjecture Tours are designated times when students are asked to re-read the classroom conjectures, discuss them with their peers, and consider counterexamples or ideas for how they can be written in more precise and clear ways.

With time, students will begin to do this analysis and justification work all on their own with the understanding that this is a very important role that they have as members of a math community.

---

Gina Picha, Ed.D. is the author of Conferring in the Math Classroom: A Practical Guidebook to Using 5-Minute Conferences to Grow Confident Mathematicians (Stenhouse, 2022). She received her master’s degree in education from Aurora University and her doctoral degree in curriculum and instruction from Concordia University-Austin.

Gina has worked in education for 14 years teaching kindergarten, first grade, fifth grade, as an elementary instructional coach, K-12 curriculum specialist and K-5 district math coordinator. She is currently a mathematics curriculum writer living in Austin, Texas with her husband Deric and two sons, Nolan and Cort.

---

Credit for images and tables: From Conferring in the Math Classroom by Gina Picha, ©2022, reproduced with permission of Stenhouse Publishers. No reproduction without written permission from the publisher.