Stick to Routines to Promote Math Reasoning

Routines for Reasoning: Fostering the Mathematical Practices in All Students
By Grace Kelemanik, Amy Lucenta, and Susan Janssen Creighton
(Heinemann, 2016 – Learn more)

Reviewed by Rita Platt

For years I’ve referred to myself as a “language arts person.” I’ve passed many a door to a math classroom and rolled my eyes at the quote that almost inevitably hangs there, “We use math every day.” Yeah, I thought, but not much more than what we learned in fourth grade.

Kelemanik, Lucenta, and Creighton’s new book Routines for Reasoning: Fostering the Mathematical Practices in All Students has made me rethink that snobby tendency. Their work, along with that of Dr. Nicki Newton, has helped me to see myself as a “math person!”

The Mathematical Practices Reordered

Routines for Reasoning: Fostering the Mathematical Practices in All Students is built around the eight mathematical practices central to the Common Core State Standards, which the authors say “beautifully summarize the way that mathematicians work” (p.1).

The authors start with an overview of the practices, but rather than presenting them linearly, they order and emphasize them in an enlightening hierarchy.

First, look at how they are presented in the Common Core State Standards:

1. Make sense of problems and persevere in solving them
2. Reason abstractly and quantitatively
3. Construct viable arguments and critique the reasoning of others
4. Model with mathematics
5. Use appropriate tools strategically
6. Attend to precision
7. Look for and make use of structure
8. Look for and express regularity in repeated reasoning

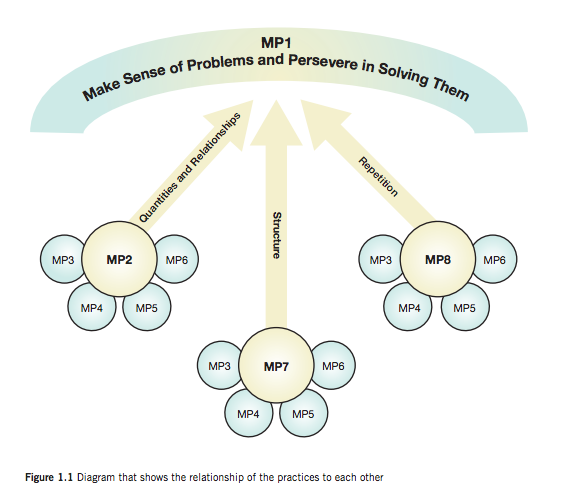
Again, Kelemanik, Lucenta, and Creighton help teachers to see the practice standards not as linear, but as hierarchical. First, they say, think of standard one, Make Sense of Problems and Persevere in Solving Them, as the star of the show. Then, look at practices two, seven, and eight as the lead actors. Last, practices three, four, five, and six are the supporting actors and fit under and together with the leads. Look at this graphic for clarity.

Reproduced with permission from Routines for Reasoning by Grace Kelemanik, Amy Lucenta, and Susan Janssen Creighton. Copyright © 2016.  Portsmouth, NH: Heinemann.

Against the Chameleon Pedagogy

Sometimes teachers, myself included, search for that wow factor, in hopes of making our lessons more exciting. Like chameleons changing colors, we change routines, methods, and strategies. This, say the authors, is not good for fostering mathematical thinking in students. When systems change, students have to use their precious attentional resources to understand the new routine rather than investing them in the mathematics.

As Kelemanik says in a video interview, “Instructional routines are an amazing support for both the teacher and the learner in the mathematics classroom…they hold the activities of the classroom steady.” They lower cognitive load, helping learners be “freed up to do the hard work of the mathematical thinking.”

The Routines

Kelemanik, Lucenta, and Creighton offer routines for working with the “lead actor” practices; two (reason abstractly and quantitatively), seven (look for and make use of structure), and eight (look for and express regularity in repeated reasoning,)

Ample examples are included to illustrate how each routine plays out in practice, and the routines follow essentially the same pattern:

1. Statement of the math practice goal
2. Time for students to think individually
3. Time for partner work
4. Full group discussion
5. Time to reflect on the mathematical practice
6. Repeated working of problems that develop the practice

Embedded in each routine are what the authors refer to as the “Four Instructional Strategies” (p, 28). Each strategy is well defined and the authors include extensive examples of each in the practical final chapter and appendix.

1. Ask yourself questions about the type of reasoning needed to solve a problem
2. Annotate the problem, highlighting and jotting notes when needed
3. Use of sentence frames or sentence starters to help students talk about math
4. The Four Rs: Repeat, rephrase, reword, and record the problem

Additionally, for each routine the authors take special care to offer commentary about how the routine can be used with English language learners and students with special needs. They are clearly interested in equity, and it is refreshing to see that concern embedded into the text frequently.

Close Reading in Math

After each routine has been explored in depth, a chapter is devoted to a routine to help students begin with and have the stamina to work through mathematical problems. The recommendation is to teach students to read problems a minimum of three times. Teachers familiar with close reading techniques applied to complex texts will recognize and appreciate this routine.

I highly recommend this book. It is not an overstatement to say that I feel indebted to the authors of Routines for Reasoning: Fostering the Mathematical Practices in All Students. I am a better teacher and thinker for having read it. My own reasoning has been fostered and I am excited to foster that same type of mathematical thinking in my students.

Rita Platt (@ritaplatt) is a Nationally Board Certified teacher with master’s degrees in reading, library, and leadership. Her experience includes teaching learners in remote Alaskan villages, inner cities, and rural communities. She currently is a teacher-librarian, teaches graduate courses for the Professional Development Institute and writes for We Teach We Learn.