First Days of Math Class: Fractions and Equations

A MiddleWeb Blog

After a wonderful three-week vacation, lots of reading for fun, sleeping late, and going to doctor and dentist appointments that I can’t fit in during the school year, I’m ready to start thinking about the coming school year.

As I begin planning start-of-year activities, I’m reflecting on some of the barriers to my students’ learning in the year just past. In general, my students struggled with two areas: fractions and solving equations. In fact, to some extent, it seems like these two topics are problem areas every year.

Card Sort to Review Fractions

From time to time I think about reviewing fractions at the beginning of the year, but I always talk myself out of it, usually because of time constraints. However, this year I plan to address it specifically in the first weeks and hopefully head off issues in the future.

I have given a lot of thought to why my students struggle so much with fractions, but I’m still not sure I have a good answer. I even hear students say they will skip a problem if it has fractions in it! I’ve wondered if it’s just a shift in societal norms – maybe we just don’t have to think in “fractional ways” so much today? (I do know that students don’t seem to struggle with the idea of decimals the same way they struggle with fractions.)

I think about my husband, who says he’s not good at math, and he is quicker with fractions in his head than I am because measuring is part of his job. My mom, who also says she’s bad at math, can quickly compute fractions in her head because she has practice related to sewing and cooking. I wonder if it’s something that is just not a big part of students’ lives anymore.

Some ideas to scaffold student thinking

I think to help students in this area I will begin with a MAP (Mathematics Assessment Project) lesson: Translating Between Fractions, Decimals, and Percents. (Found here under Grade 6 or jump here.) This activity is a card sort that will require students to “Compare, convert between and order fractions, decimals, and percents.”

Students will be given cards with decimals and percents and will have to place them in order from least to greatest, and also fill in some blank spaces. Next they will be given cards with different areas, and they have to match them to the decimals/percents cards, making sure to put them in order from least to greatest. They will repeat this procedure for the fractions cards and the scales cards.

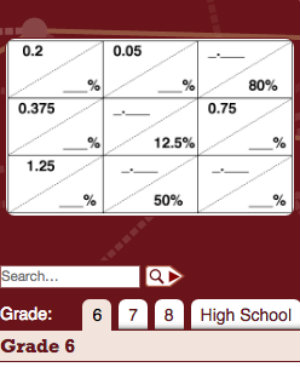
My plan is to do this in the first week of school. It will help me determine what sort of mastery they have with fractions, and it will get them in the habit of working through MAP’s activities, which I plan to implement throughout the year. By doing this activity at the beginning of the year, I hope my students refer back to it throughout the months ahead to help them reason on problems that require them to use fractions.

Playing Games to Help Students Master Equations

According to a new Stenhouse book Accessible Algebra, written by Anne M. Collins and Steven R. Benson (which I read over the summer and is awesome!), students need to “have an opportunity to ‘play’ with equations using mobile balances, puzzles, and games.” So I plan to incorporate an activity from this book titled “Gauss and Figurate Numbers.”

In short, the activity will require each student to fist bump with every other student in the class (purposefully not telling students to count how many fist bumps are exchanged). The students will then be asked to calculate how many fist bumps would be exchanged in a class of 28 students and list and show what strategies they used to come up with an answer. (Check out the activity here.)

I like this activity for several reasons. For one, it lets them practice finding the correct equation to model this situation. In addition, it will give my high school students some foreshadowing regarding quadratics, and in fact I plan to revisit this problem when we begin our unit on quadratic functions. Finally, there are several different ways a student could work this problem, and I believe the students are going to have to work together to arrive at a correct answer.

I think this will be a great activity for the first day. As students exchange fist bumps, they can also exchange names and it will serve as a little meet and greet.

Rules for Solving Equations

I stumbled across a blog post written by Glenn Waddell, My Three Rules of Mathematics. The post dealt with how to use three simple rules to help students solve equations. The post recommended introducing the three rules at the beginning of the year and referring back to them throughout the year. I really liked this idea! However, instead of giving the three rules to my students I plan to let them, as a class, create their own rules for solving equations.

My plan is for students to work with a partner to solve various equations. As they solve the equations, they should be thinking about what steps and processes they are using to correctly solve the equations, and each pair of students will create their rules for solving equations.

At the end of the class, a gallery walk will allow the students to look at each other’s work. To conclude we will come back together and devise a set of rules or procedures for solving equations as a class. I think giving them that extra ownership will make the rules more meaningful to them. I plan to post their rules and keep them up for the entire year for us to refer back to and possibly revise if necessary.

To reinforce these concepts throughout the year, I plan to continue to use my low tech strategy with sticky notes (Not Yet, Almost There, Got It!) along with quizzes, and test questions throughout the year.

If anyone has ideas or suggestions to help students master fractions or solving equations, please share in the comments below!

Feature image: Andertoons.com