How Open-Ended Math Problems Keep on Giving
Imagine an open-ended math task that gets students asking questions as well as answering them. Each student works at the level of her current ability and interest, but no one finishes, because there are always new questions to ask!
A problem like this would help you differentiate instruction for advanced learners while stimulating curiosity, deep understanding, and perseverance for all learners.
I call these tasks “problems that never end.” They are a type of High Cognitive Demand task, and they need not be traditional story problems. In fact, a story problem is not really a problem at all if you have been taught a procedure for solving it. By definition, a problem is something that you have not been taught how to do!
Here’s an example
I have used the image below for many years with learners of all ages. What do you think the problem might be? How would you begin solving it? Try it before reading further!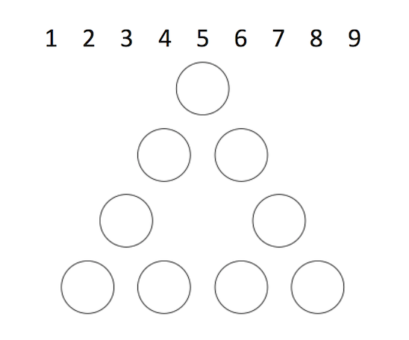
Keeping the problem going
This is a great problem, but does it really go on forever?
Let’s explore my version of the problem a bit more. Suppose you have found a solution. (Maybe you have!) Imagine some new questions that you or your students might ask.
Here are some possibilities:
- How many solutions are there? What do they have in common? What counts as a new solution? How many solutions are there if I count every small variation as a new solution? Can I find more than one solution strategy?
- Why are the corner numbers important? What do I know about them? How can I prove it? Is my sum the only possible one? What is the smallest possible sum? The largest? Can I make every sum between the smallest and largest?
- Can I use my existing solutions to help me find solutions for other sums? How many of those are there? Are there patterns that will help me make predictions quickly?
This long list of questions may look overwhelming at first. Fortunately, when you teach, you won’t be dealing with all of them at once! When the questions grow naturally out of the exploration process, they are not so daunting; rather, they are exciting and full of possibility.
By the way, if you think this list is impressive, look here for more questions (you can also download my Triangle Sums handout). The possibilities are virtually endless, because new discoveries keep leading to new questions!
I have never yet had a student who has run out of things to explore. They simply reach a point when they are ready to move on to something else. I often like to press them just a little beyond this point. They are usually capable of more than they believe, and once they get past a stumbling block, they are off and running again!
Reflecting on the experience
Take a moment now to reflect on your experience with the image. You probably did some open-ended noticing and wondering before you even started solving your problem. These processes are at least as important as remembering and practicing mathematical procedures.

It also changes the way you think about teaching. Rather than worrying about learning every detail before you teach it, you enrich your own understanding of math through teaching. James Tanton of the Global Math Project advises allowing yourself to be vulnerable: “be your honest true self in front of students. Wonder about math; be honest if you don’t know the answer and then help students try to find it.”
The versatility of open-ended problems
Is it hard to imagine your students sticking with one problem for so long? Think of this challenge as an opportunity. Learning to persevere with tasks that take significant time and effort is an important new skill for many students. Remember that you are nurturing new habits. You may sometimes have to sell the problem to your students, but it may not be as hard as you think. Students are naturally curious about their own ideas and questions – and your excitement will be contagious!
How can you teach this way when you have a long list of math standards to cover? Think for a moment about which math standards our “triangle of circles” problem might address.
- Young students will learn about properties of addition and subtraction.
- Older students can investigate counting strategies and symmetry as they count solutions and explore relationships among them.
- High school students can create and analyze algebraic expressions to express patterns they discover.
All students develop crucial reasoning skills. The problem differentiates instruction naturally, because students enter and pursue it at their own levels.
Getting started
These problems last a long time, and they tend to deal with many concepts at once, so you will probably not need too many of them. Nevertheless, it may take time to build a collection that thoroughly addresses the standards you teach. You will probably need to build your collection gradually. The images and notes below suggest some possibilities to start with. Look here for more notes on these tasks.
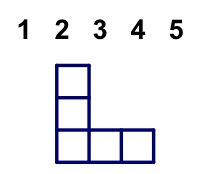
How can you get from 64 to 2 using only these operations?
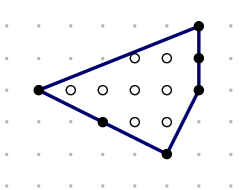
What do these shapes have in common?
What is special about the large black dots? What is special about the open dots? What is the area of the polygon?
The Torrans are a species from another planet. How do their numerals work?
from Advanced Common Core Math Explorations: Numbers and Operations. Routledge/Prufrock Press. Used by permission.
from Advanced Common Core Math Explorations: Ratios, Proportions, and Similarity. Routledge/Prufrock Press. Used by permission.

from Advanced Common Core Math Explorations: Factors and Multiples. Routledge/Prufrock Press. Used by permission.
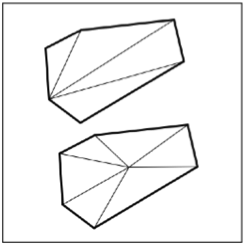
What are the measures of the star-tip angles?
from Advanced Common Core Math Explorations: Measurement and Polygons, Routledge/Prufrock Press. Used by permission.
I hope you feel inspired to try some never-ending problems with your students, and I invite you to find, create, and share some of your own.
Further resources for problems that never end
Advanced Common Core Math Explorations book series, by Jerry Burkhart. Routledge/Prufrock Press.
Exploding Dots, by James Tanton
Extending the Challenge in Mathematics, by Linda Jensen Sheffield. Corwin, 2003.
Intrepid Math, by Jerry Burkhart
K–8 Math Projects, by Jerry Burkhart

As founder of 5280 Math Education, he helps schools and districts implement research-based programming for gifted math students and offers tools and strategies for developing and nurturing adventurous math learners. Visit his store at MyEdExpert.


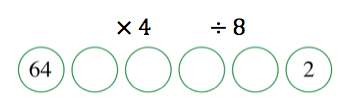




































I like how you went deeper into the problem of the triangle numbers. When I started with the triangle problem my granddaughter, 3rd grade come up with other extensions such as larger triangles, squares, and other shapes. Here is a document with some of those extensions. https://docs.google.com/document/d/1GCWO1ucoszLA73jPz_yhwV05dDb5cOvzHPugfsPWNHk/edit?usp=sharing