How Important Is the “Why” in Math Class?
A MiddleWeb Blog
I recently listened to a podcast (Mr Barton Maths Podcast; Ed Southall: Part 1), and part of the conversation dealt with the importance of explaining the why as opposed to just instructing students on the steps or giving them an algorithm that works.
For example, when learning how to divide a fraction by a fraction, many students are taught “Keep, Change, Flip” – keep the numerator the same, change to multiplication and flip the denominator.
Is this sufficient or is it important for the students to know why “Keep, Change, Flip” works? (If you are interested in exploring the topic of dividing fractions by fractions, and why inverting and multiplying work, I have listed some resources below. There are several topics where I found the WHY to be particularly relevant, such as fractions, operations with signed numbers, multiplying binomials, and factoring).
The discussion on the podcast sparked two questions in my mind:
- What are the benefits of explaining WHY to our students?
- Is there a right way and a wrong way to explain the WHY to our students?
The Benefits of Explaining the WHY
1. Deepen Student Understanding
I recently taught students that when you multiply a negative by a negative your product is positive. I’m embarrassed to say that I did not teach them why it works, only that it does work. It never occurred to me to think about why it worked. I’ve taught it for so long I have forgotten to ask myself why.
As a result, I missed an opportunity to help students really understand the concept. There are so many great strategies I could have shared with my students – all related to why multiplying a negative with a negative has a positive product. The same goes for adding and subtracting signed numbers, which I taught in the same unit. (Here is a good resource from the NCTM Math Forum.)
2. Help Improve Student Retention
Often when students rely on memorizing problem solving steps without an understanding of why, they cannot retain the information. In fact, when my students were tested on adding/subtracting and multiplying signed numbers, some forgot the rules altogether or remembered them incorrectly. If I had given them a stronger foundation, they would have at least had the ability to reason through the problem.
In my Algebra 2 (with Trig) class I put this problem on the board:
Full disclosure: my students tend to struggle with fractions. I could hear them talking among themselves about how to solve the problem (without a calculator) of 1/2 ÷ 2/3. As a class we talked about “Keep, Change, Flip,” and some of them remembered being taught that phrase or something similar. However, even the students who remembered the phrase couldn’t quite remember how to execute those steps.
I showed them how “Keep, Change, Flip” worked and heard students say things like, “oh yeah” or “I remember now.” And they did. I am sure if I had given them a worksheet full of similar problems they could have worked them.
We then started talking about the WHY, and we discussed the convenience of making the denominator a 1 by multiplying by the reciprocal. (I shared what I learned from the podcast guy Ed Southall’s book Yes, But Why? Teaching for Understanding in Mathematics.) This seemed to make sense to the students.
I then asked them if they thought knowing why “Keep, Change, Flip” worked would help them remember how to work this type of problem in the future. About half of the students said it would, and about half thought it would make no difference.
During the course of the discussion some students said that they were not interested in knowing why; they just wanted to know the steps. One student said it was overwhelming when teachers tried to tell them too much. A few students said they did better if they knew why, and one student said that it was very important for them to be told why. This student felt like knowing why was necessary for them to be successful.
3. Improve Student’s Confidence
Many students recognize that memorizing steps is the not the same as understanding or mastery. Knowing why something works can help struggling students gain a sense of confidence.
My daughter shared with me recently that she never felt like she was good at math (despite always making A’s or B’s throughout her high school and college math classes) because she could follow the procedures, but she never understood why she was doing them. If she felt that way, that means that there could be some students in my class right now that are mastering the process/content but don’t feel like they are good at math because I haven’t sufficiently explained the principles behind what they are learning.
The Right and Wrong Way to Explain Why
I think in the past I have been guilty of too much too soon. The situation is like this: I get excited about explaining the why of fractions, Pythagorean Theorem, quadratic formula, or unit circle, and begin a lengthy explanation about the why. I look out at my students and everyone is either confused or uninterested.
After thinking about it, I realize this usually this happens if I try to explain why something works before I have given students a chance to practice how it works. For students that may be struggling, I think this cart-before-horse approach is a recipe for disaster.
In fact, a British article titled How can teachers help students overcome their fear of maths? states, “There is evidence that even strong students of maths can feel daunted and overwhelmed when there is too much information at once and not enough time to practise.” My recent conversation with my own students bear this out. They actually told me too much information too soon is overwhelming.
So timing is key. In the future, I plan to delay explaining the WHY until students have some experience practicing with the steps. At times students do ask why something works the way it does, and I think it can appropriate to address it with the whole class when that happens.
It’s My Job to Explain Why
As a teacher, it’s my responsibility to be ready with a clear and concise explanation for the WHY. With that goal in my mind, I plan to keep a notebook with all of my Why’s for each unit I teach. I already have student-friendly explanations about the Why of dividing fractions by fractions and multiplying a negative times a negative!
If you are curious about the subject, I have listed some resources here. And if you have ideas about teaching the Why from your own classroom, please share.
► Yes, But Why? Teaching for Understanding in Mathematics by Ed Southall
► Nix the Tricks: A Guide to Avoiding Shortcuts That Cut Out Math Concept Development by Tina Cardone
► NCTM’s The Math Forum: Ask Dr. Math
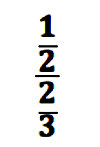
Great points! Explaining “why” first teaches students to tune out until we get to the active part. Inquiry-based learning (IBL) teaches concept at the same time as procedure: like a road map as opposed to GPS. I’m piloting CPM IBL, and my students are engaged from the moment they’re logged in. But, I think it’s easiest for many teachers to wade into IBL gradually. Collecting vetted IBL activities organized by grade/topic here: https://gotgettransfers.wordpress.com/
Thank you for your comment! And thanks for the link- it looks like a great resource!
inquiry-based learning is something that elementary math teachers have been working on in my district for some time. In fact we strive for the students to figure out the why vs. us telling them. Students know they will be asked to explain and justify their reasoning. It understandably gets harder when the concepts become more abstract in High School, but it is worth the effort. Our students believe that mathematics is something that they can make sense of and that it should make sense. Many students say math is their favorite subject!!
Thank you for your comment! You are so right, math should make sense to students. I know your elementary math teachers are giving their students a great foundation!
Even better – have the students explain why – they should be explaining why strategies work all the time and comparing two strategies together… why do BOTH of these strategies work? #MathChat #ImpactTeams
Good point! I agree, helping students get to the point where they can explain why and compare the advantages/disadvantages of different strategies should be the end game for all teachers. Thanks for your comment!
Check out the new middle school math curriculum from Illustrative Mathematics at https://im.openupresources.org/. Instead of having teachers explain why, the problem-based curriculum builds concepts slowly and purposefully so that students experience the “why” as they extend their thinking. See also Bill McCallum’s blog http://mathematicalmusings.org/ for a thorough and outstanding discussion of fraction division.
Thank you for your comment! I like what you said about curriculum helping students develop their the why. I have had a chance to look at a few of the lessons from the new curriculum from Illustrative Math and they look so good! I cannot wait for the high school curriculum to be released! Thanks for the link concerning fractions, I found the diagrams to be especially useful. Thanks for sharing that resource, I am going to add it to my collection.
I completely agree with the idea that the “why” is important.
The order of when the “how” and the “why” is taught may also be very important. The following research looks at the possible downsides of learning “how” first:
Interference of Instrumental Instruction in Subsequent Relational Learning
Dolores D. Pesek, David Kirshner
To balance their professional obligation to teach for understanding against administrators’ push for higher standardized test scores, mathematics teachers sometimes adopt a 2-track strategy: teach part of the time for meaning (relational learning) and part of the time for recall and procedural-skill development (instrumental learning). We explore a possible negative effect of this dual approach when relational learning is preceded by instrumental learning. A group of students who received only relational instruction outperformed a group of students who received instrumental instruction prior to relational instruction. Interview data show aspects of cognitive, metacognitive, and attitudinal interference that may have been caused by the juxtaposition of instructional modes.
The article can be found in the following NCTM publication:
Lessons learned from research / edited by Judith Sowder and Bonnie Schappelle.
Thank you for the comment! I share some of your concerns regarding teaching both procedures and teaching for understanding, that’s one of the reasons I wanted to write this article. As you alluded to, teachers are tasked with having to prepare students for high stakes tests and that certainly guides some of the instructional decisions that I make. I look forward to reading the article you referenced in full, I’m interested in the logistics of the study, sample size, age of students involved, etc. Thanks for sharing such relevant research!
The why teaching strategy is very important as explained by the author of this post. Laying a strong foundation in math by explaining why a problem is done in that particular way should be emphasised at all levels of learning.
Thank you for your comment! I agree all levels of learners benefit from understanding the why behind math concepts.
Thanks for your post! I chose to create my professional growth goal around this topic for the year after reading your blog post in the fall.
The middle school math curriculum that was chosen by our district provides students with “why” the algorithms work on a regular basis. I purchased “Yes, but Why?” and was happy to see that most of the models were familiar to me from the software that we use. I wasn’t really aware of this until I began reading the book.
I also felt that being strong in math allowed me to feel confident that the strategies that the book used when it came to many topics. For example, I am constantly reminding my students to replace “times” with the word “of” in multiplication. This allows them to know when they see the word “of” in a word problem or when dealing with percents to use it, and most do automatically now.
I will say that for some of my students the “why” is much more easily grasped, but most of my day is spent with students in need of math intervention. For some teachers, I believe they think trying to explain “why” an algorithm works is over their heads, I’ve seen this year that it’s definitely beneficial to all students using models and manipulatives to understand the process they’ve been taught. Giving those struggling students a visual of “why” allows them to grasp the topic better, because they see why the process works. It becomes less rote and more internalized which means that their deeper understanding allows them to really know the process. We can go back to a topic (for example multiplying fractions) several weeks later, and they recall the process of shading and putting the models on top of one another, and that triggers their memory.
I was very pleased with this choice of personal development this year and am happy to have used this in the classroom. Thanks!
Thank you so much for your comment! I am so impressed with how you are teaching your students to have a deeper understanding of the “why”. I feel like you are probably further along in this journey than I am, but it is something I plan to work on more this year. Also, I really liked your comment related to vocabulary (using “of” instead of “times”), I think that helps lay a strong foundation for students. Thanks again for sharing!
Mathlete here. I hated math as a kid. I hate arbitrary rules, I always did. So when someone told me “this is the rule,” I always asked why. My teachers got tired of telling me why. I was even given disciplinary merits for being a constant disruption. As a teen, I taught myself how to code, mostly because I wanted to develop video games (and did for awhile in the future, but I digress).
I became a proficient developer in my career. At first, I only did as much math as was required, but I began to use the resources at my disposal to understand how the math actually worked and why. And I caught the bug big time.
Now after some years in IT, I’m tired of business production and am going back to school.
For math.
And because coding has an intrinsic why requirement, math has become sublimely easy, as I apply the principles of logical analysis to math.
I feel cheated of the time I spent in why-less math classes. I got here the long way. But I’m here and I’m hooked.
The why is essential.
As a teacher I always enjoyed explaining the why, to the point where I realised I was overwhelming my students. When I got to the explaining of the actual steps of how to do something, they would just be exhausted and confused. The concept of reversing that order, explaining the steps first, giving them chance to practice and then explaining the why is very eye opening to me. Thank you, I will give it a shot.