10 Tweaks That Can Deepen Math Tasks
By Jerry Burkhart

Take a minute to look at these math tasks. What do they have in common? What will students learn?
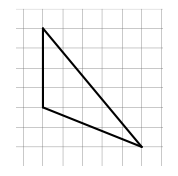
Find the area of the triangle.
Find the product.
Calculate the value.
Find the slope of the line.
Solve the equation.
Did you notice that you could complete each of the tasks by performing a memorized procedure? Now notice what happens if you add the phrase “Write a story…” to your directions. For example:
• Write a story about the triangle and its area.
• Write a story about the expression 6 • 2/3.
• Write a story about 15% of 48.
• Write a story about the slope of the line.
• Write a story problem for the equation 3x – 7 = 1
With this small change, you have encouraged your students to (1) make a connection to their experience, (2) think about the meaning of a concept, and (3) apply creativity to a math problem!
As a teacher, you gain something valuable from the experience, too – a window into your students’ mathematical thinking. Looking at their work on traditional, formulaic tasks may give you a glimpse of their misconceptions, but observing students as they engage with deeper tasks shows you their conceptions – the ideas that they bring to the table.
More Strategies
Write a story is one of a set of ten strategies I’ve devised for transforming traditional math tasks into deep, meaningful activities.
- Write a story.
- Draw a picture.
- Explain why.
- Find another way.
- Compare and contrast.
- Start with the answer.
- Remove information.
- Solve to learn.
- Build a pattern.
- Ask “What if…?”
I call this collection of strategies Ten Plus One (see this free download). More about the “plus one” part later. You may use the strategies alone or in combination. For example, the second and third strategies, draw a picture and explain why, often work well with write a story. For a calculation such as 6 • 2/3, your new task might be:
(1) Create a real-world story for the expression 6 • 2/3.
(2) Draw a diagram that fits your story.
(3) Explain why your story and picture show the meaning of 6 • 2/3.
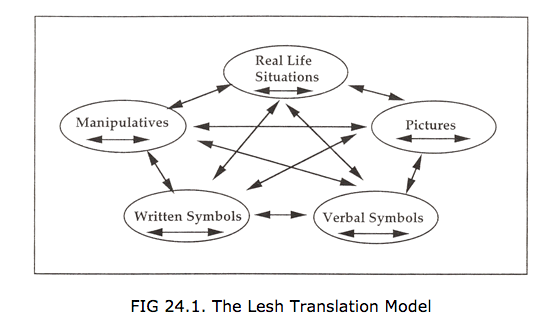
These three strategies alone form a flexible framework for deepening students’ understanding of math concepts. They are related to the Lesh Model, and there are some nice templates available (Modeling Math Meaningfully and the Lesh Model Template) to use with your students.
The fourth strategy, find another way, encourages students to think flexibly. For example, there are many ways to do a calculation like 15% of 48. Find another way works especially well for students who have completed a task and are waiting as other students continue working.
I love using this strategy, because I get to hear an endless variety in my students’ ideas. No matter how well I think I know a concept, I always gain a richer understanding by listening carefully to my students. (For an excellent blog on listening to students, see mathontheedge. Michelle Russell also has a great MiddleWeb post!)
The Look and Feel of Deep Math Tasks
The Ten Plus One strategies “open up” students’ thinking by shifting the focus from facts, procedures, and performance to patterns, relationships, and meaning. In her book Mathematical Mindsets, Jo Boaler argues persuasively that the latter focus is the truer representation of what it means to “do math.” Furthermore, this way of thinking about math makes it accessible to all learners while supporting those who need further challenge.
The fifth strategy, compare and contrast, is excellent for focusing on patterns and relationships. For example, if students are studying areas of parallelograms, they might compare and contrast the following figures:
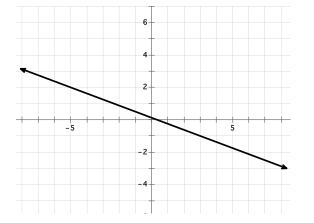
If they are studying slope, they may compare and contrast the slopes of these lines:
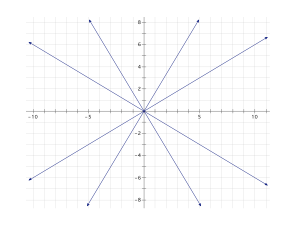
You could also have students generate items to compare and contrast by using some of the later strategies. For example, rather than asking students to solve an equation such as 3x – 1 = 7, you might start with the answer of 2 2/3 and challenge them to find multiple equations having that solution (the sixth strategy).
Or, beginning with a task like 128 ÷ 16 = ___ , you could remove information (the seventh strategy) to obtain 128 ÷ ___ = ___. (Try asking for non-whole-number responses, too!) Both modified tasks now have multiple solutions with interesting relationships worth comparing and contrasting.
Over time, as you use continue to use strategies like these, you begin to notice new patterns in the types of questions that you and your students ask. To me, these changes have come to define deep mathematical learning.
 Learning along with students
Learning along with students
Whenever I create a new task using these strategies, I try it myself. Though my goal is to anticipate my students’ thinking, I often gain new insights into the mathematical content. I have seen this happen with other teachers as well.
In one of my presentations, I remember a teacher who chose to use the compare and contrast strategy on the task “Find the factors of 42.” When he wrote out the factors and began comparing them, he discovered relationships between the factors that he had never noticed before, and he could hardly wait to share and further explore his own discoveries with his students!
For example, before teaching formulas for interior angles in polygons, you might give students a few tools (such as rulers, compasses, and protractors) and ask them to draw a regular pentagon. I have gained many new insights about relationships between angles in polygons by watching students tackle this problem!
Exploring further
Strategies nine and ten involve creating patterns and asking what happens when you change numbers, operations, words, etc. in a problem. I invite you to explore these strategies in the Ten Plus One document. There you will also learn about the “Plus One” part of the name (which has to do with complexity) and find more information and resources to support your work.
Though I originally compiled the Ten Plus One strategies in response to teachers’ requests for support in creating tasks that meet needs of advanced learners, it is a useful tool for all students. Thinking deeply is an important and realistic goal for all math learners, and while it may take a new mindset and a little courage, it can be an exciting, ongoing journey of discovery for both you and your students.
Resources related to mathematical depth
► Advanced Common Core Math Explorations book series, by Jerry Burkhart. Prufrock Press, 2014–2017.
► All the Mathematical Methods I Learned In My University Math Degree Became Obsolete In My Lifetime, an article by mathematician and author, Keith Devlin
► Extending the Challenge in Mathematics, by Linda Jensen Sheffield. Corwin, 2003.
► Mathematical Mindsets, a book by Jo Boaler, 2015
► youcubed (website)
Inexpensive ($5) lessons/projects by Jerry Burkhart:
___________________

As founder of 5280 Math Education, he helps schools and districts implement research-based programming for gifted math students and offers tools and strategies for developing and nurturing adventurous math learners. Visit his store at MyEdExpert.

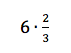
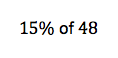

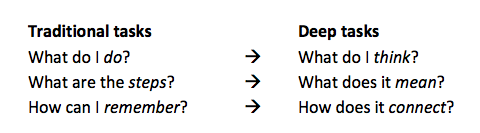 Learning along with students
Learning along with students





























Loved this post! So many great ideas I can take to my classroom tomorrow for making math more accessible, challenging and engaging. I’ve now got a ton of tabs open to further explore the links you shared here. Thanks for sharing!