2 Key Math Strategies for Students with Disabilities
By Bradley Witzel, Ph.D. and Barbara R. Blackburn, Ph.D.
Much effort is made in schools to help students with disabilities gain employment skills, improve behavior, and build reading skills to assure ongoing learning and social independence.
While these emphases are important, mathematics is often a forgotten part of special education. However, mathematics is one of the most important predictors of student performance and adult successes.
Specifically, proficiency with Algebra 2 is a strong predictor of technical school completion, which grants licensure in such highly needed areas as air conditioning repair, auto mechanics, welding, etc.
Late elementary and middle level math performance in computation of whole and rational numbers is a predictor of algebra performance. Early numeracy is a predictor of not only late elementary math performance but reading performance as well.
Thus, math instruction for students with disabilities should include research-supported approaches to maximize student proficiency (understanding and procedural knowledge) and intervention should be aimed at helping students recover any lapse in understanding.
Several research-supported approaches have proven effective for students with special needs and mathematics difficulties. Among those are two we recommend: the concrete-visual-abstract sequence of instruction (CVA) and schema-based problem-solving instruction (SBI).
CVA Is a Three Step Model
The concrete-to-visual-to-abstract sequence of instruction (CVA) is a research-supported, three-step model that uses a series of learning modalities to help students build abstract understanding of mathematics. CVA is also known as CRA (Concrete-Representational-Abstract) and CSA (Concrete-Semiconcrete-Abstract) and has been shown effective for learning such mathematics concepts as number sense, whole and rational number computation, simplifying algebra expressions, solving algebra equations, and solving geometric principles.
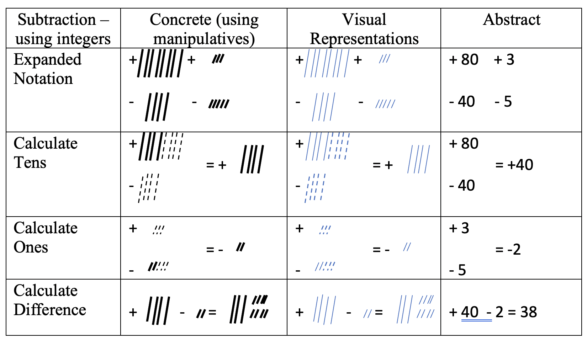
CVA starts first by solving a math problem using concrete objects followed by solving similar problems using visuals and then abstract notation alone (Witzel & Little, 2016). Because movements between phases of learning are fluid, it is helpful to show abstract notation while teaching using concrete and visual representations. This explicit connection aids in the transition from concrete to visual to abstract phases of learning because the abstract notation is present at each stage.
While CVA seems fairly straight-forward, it requires precision of instruction and thoughtful planning. We recommend the following steps when developing and delivering CVA:
To understand the importance of the link between the different phases of learning, using the same construct as presented earlier, the student solves multi-digit subtraction, 83 – 45, using the integer rule.
At the concrete phase, the student decomposes the minuend and subtrahend. Next, the student computes the tens by comparing the minuend and subtrahend to reach +40. Then the student computes a similar comparison with the ones place to find -2.
Finally, the student calculates the difference between the tens and ones differences to equal 38. This process and the number of steps matches across phases to show a parallel approach.
CVA is a powerful way to help students solve computational problems, and it is adaptable to many different types of problems.
SBI targets math word problems
While CVA is effective for building computational proficiency, schema-based instruction or SBI is effective for solving word problems. With the increased use of word problems on mathematics standardized exams, schools, districts, and states have increased their emphasis on effectively teaching students how to solve them.
Solving word problems often requires students to decode complex vocabulary, comprehend a paragraph of text, access background knowledge of authentic events, plan multiple steps and accurately compute problems. Despite its popularity, using “keyword” as the lone strategy has shown little to no effect on word problem performance.
One of the most effective word problem solving approaches is schema-based instruction (Witzel et al, 2021). SBI has a four-step approach: problem identification, problem representation, and problem set-up, followed by solve and check.
When enacting the problem solving steps for SBI, using a consistent attack strategy helps guide students through the problem solving approach. One such attack strategy that matches SBI is DOPS.
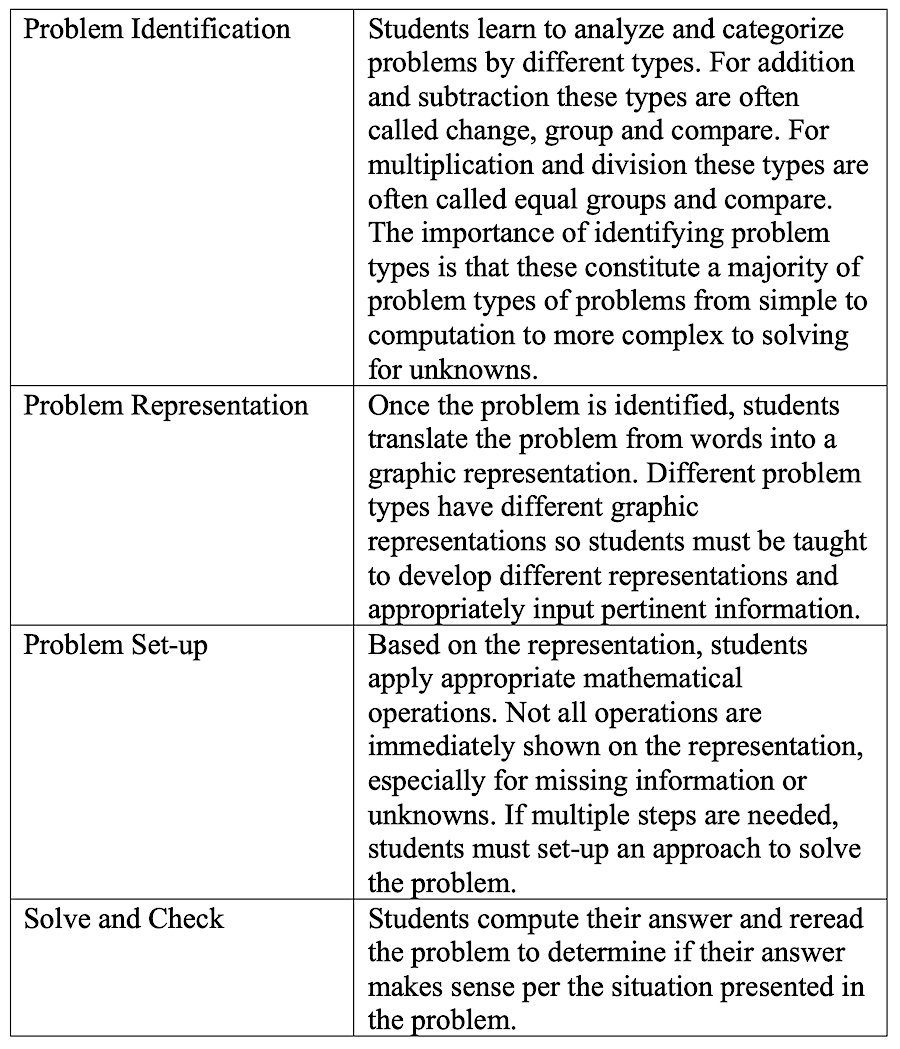
D = Determine the problem type
O = Organize the information using the schematic diagram
P = Plan to solve the problem
S = Solve the problem arithmetically
Using cognitive approaches like DOPS helps with students who struggle with executive functioning and planning by building in self-regulation (Witzel, 2020).
How to implement the SBI strategy
To show how to implement SBI using a cognitive approach like DOPS, we highlight multiplication and division problem solving. The two most general types of multiplication and division problems are equal groups and comparison.
Equal groups problems will present up to two components in word problems – number of groups and number of items per group – leading to a total number or amount. Equal groups representations look like this:
Example: Emily unloads 8 boxes of books at school. There are 12 books in each box. How many books does she unload?
Determine problem type – This is an equal groups problem because there are equally sized boxes of books.
Organize a representation, such as the one below.
Plan to solve, 8×12
Solve and check = 96 books makes sense considering the number of boxes.
Comparison problems will also present up to two components in word problems – two items that are being compared and how many times one is greater or less than the other. Comparison representations look like this:
Example: Kelly read 9 books over summer break. Todd read 3 books. How many times more books did Kelly read than Todd?
Determine problem type – This is a comparison problem because we are talking about how many books Kelly read compared to Todd.
Organize a representation, such as the one below (T=Todd).
Plan to solve – Since this is not a straightforward computation, the student would have to analyze the problem to determine to divide 9 by 3.
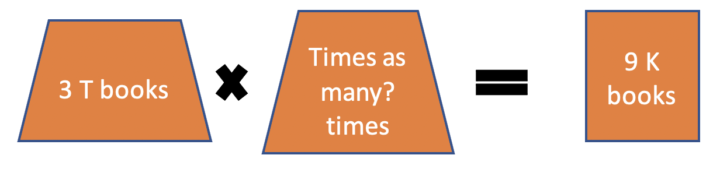
Solve and check = 3 times as many books makes sense considering Kelly read 9 and Todd read 3.
Implementing SBI is not always easy since textbooks are rarely designed to systematically teach word-problem solving. Therefore, it is important to first present problems that fit with the SBI more easily before scaffolding to more complex problems.
If students are taught SBI early, they are more likely to have success with word problems early and transition that success to later mathematics (Jitendra et al., 2013).
Conclusion
Mathematics can be a challenging topic to learn and to teach. Implementing instruction that is grounded in empirical research is highly important to maximizing success for all learners, especially those with special needs.
It’s equally essential that we formatively assess every math student through the year to learn where they are succeeding in their approach and where they are not. Using the information we gather, we can target instruction using effective instructional strategies, such as CVA and SBI, and not only help them succeed in our math classes but help them grow academically for years to come.
References
Blackburn, B., & Witzel, B. S. (2022). Rigor for students with special needs. (2nd ed.). Routledge.
Jitendra, A. K., Dupuis, D. N., Rodriguez, M. C., Zaslofsky, A. F., Slater, S., Cozine Corroy, K., & Church, C. (2013). A randomized controlled trial of the impact of schema-based instruction on mathematical outcomes for third-grade students with mathematics difficulties. The Elementary School Journal, 114(2), 252–276.
Witzel, B. S. (2020). Executive functioning disorder and mathematics: Three strategies to implement. Attention, 27(5). 19-21.
Witzel, B. S., & Little, M. E. (2016). Teaching elementary mathematics to struggling learners. New York: Guilford Press.
Witzel, B., Myers, J. A., & Xin, Y. P. (2021). Intensifying word problem solving for students with math difficulties. Intervention in School and Clinic. https://journals.sagepub.com/doi/10.1177/10534512211047580
Witzel, B. S., Riccomini, P. J., & Schneider, E. (2008). Implementing CRA with secondary students with learning disabilities in mathematics. Intervention in School and Clinic, 43(5), 270-276.
Barbara R. Blackburn, a “Top 30 Global Guru in Education,” is a bestselling author of over 25 books and a sought-after consultant. She was an award-winning professor at Winthrop University and has taught students of all ages. In addition to speaking at conferences worldwide, she regularly presents virtual and on-site workshops for teachers and administrators. from Routledge/Eye On Education.
Bradley Witzel is the Adelaide Worth Daniels Distinguished Professor of Education at Western Carolina University and has worked as a classroom teacher and before that as a paraeducator with high-achieving students with disabilities. He has written nine books and over 50 other professional publications, developed over 20 multimedia resources, and delivered over 500 presentations and workshops.
Barbara and Brad are the authors of Rigor for Students with Special Needs, 2nd edition from Routledge/Eye On Education.
